Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBID và ΔCIA có
IB=IC
\(\widehat{BID}=\widehat{CIA}\)
ID=IA
Do đó: ΔBID=ΔCIA
b: Xét tứ giác ABDC có
I là trung điểm của AD
I là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: BD\(\perp\)AB

Mình vẽ nhầm hình nha, để mình vẽ lại ở dưới cái nào để chữ vẽ lại thì bạn vẽ cái đó
Đây là bài làm
a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đói đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM

la sao eo hieu anh oi em moi lop 5 anh lop 7 saoe lam dc ha troi,voi lai bai do cau hoi giong em nhung bai em la tim ti so % cua AI va IC anh lam dc ko giai giup em voi anh.Anh ko giai dc xung dang lam gi la lop 7 ha anh,em noi co dung ko????EM NOI VAY LA DUNG CHINH XAC,DUNG CCMNR!!!!!!!!!!!!:))))))
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng:
a) AM=IK
b) Tam giác AMI bằng tam giác IKC
c) AI=IC
Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR
a) BD= CE
b) tam giác OEB bằng tam giác ODC
c) AO là tia phân giác cua góc BAC
Được cập nhật 41 giây trước (20:12)

a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đối đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
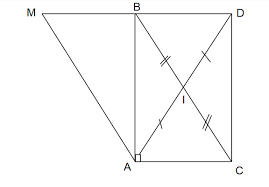
Bạn ơi, vì mình k thể kí hiệu góc. Nên bạn tự ghi góc vào bài làm của mình nhé

a: Xét ΔBID và ΔCIA có
IB=IC
\(\widehat{BID}=\widehat{CIA}\)
ID=IA
Do đó: ΔBID=ΔCIA
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: BD\(\perp\)AB

Cm : a) Xét tam giác BID và tam giác CIA
có BI = CI(gt)
góc DIB = góc CIA ( đối đỉnh)
DI = AI (gt)
=> tam giác BID = tam giác CIA (c.g.c)
b) Tam giác CIA = tam giác BID (cmt)
=> góc C = góc IBD ( hai góc tương ứng)
Mà góc C và góc IBD ở vị trí so le trong
=> AC // BD
=> góc A + góc B = 1800 (trong cùng phía)
=> góc B = 1800 - góc A = 1800 - 900 = 900
=> BD \(\perp\)AB
c) Ta có : góc DBA + góc ABM = 1800 (kề bù)
=> góc ABM = 1800 - góc DBA = 1800 - 900= 900
Ta lại có : AM // BC (gt)
=> góc CBA = góc BAM (so le trong)
Xét tam giác BAM và tam giác ABC
có góc BAM = góc CBA (cmt)
AB : chung
góc CAB = góc ABM = 900 (cmt)
=> tam giác BAM = tam giác ABC (g.c.g)
d) tự làm
Em tham khảo nhé!
Câu hỏi của Vy Hà Khánh - Toán lớp 7 - Học toán với OnlineMath