Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, ΔABD có BA = BD (gt) và ˆABDABD^ = ˆABCABC^ = 60o60o
⇒ ΔABD đều (đpcm)
b, ΔABD đều ⇒ AB = AD
Xét ΔAHB và ΔAHD có:
AH chung; AB = AD (cmt); HB = HD (H là trung điểm của BD)
⇒ ΔAHB = ΔAHD (c.c.c)
⇒ ˆAHBAHB^ = ˆAHDAHD^ mà 2 góc này kề bù
⇒ ˆAHBAHB^ = ˆAHDAHD^ = 90o90o
⇒ AH ⊥ BD (đpcm)
c, ΔABD đều ⇒ AB = BD = AD = 2cm
⇒ HB = HD = 1cm
⇒ HC = BC - HB = 5 - 1 = 4cm
ΔAHB vuông tại H ⇒ AH = √AB2−HB2AB2−HB2 = √22−1222−12 = √33cm
ΔAHC vuông tại H ⇒ AC = √AH2+HC2AH2+HC2 = √3+423+42 = √1919cm
a) Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Xét ΔBAD cân tại B có \(\widehat{ABD}=60^0\)(gt)
nên ΔBAD đều(Dấu hiệu nhận biết tam giác đều)
b) Ta có: ΔBAD đều(cmt)
mà AH là đường trung tuyến ứng với cạnh BD(gt)
nên AH là đường cao ứng với cạnh BD(Định lí tam giác cân)
hay AH\(\perp\)BD(Đpcm)

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

e) vì AC vuông góc vs BK , KE ( kéo dài ED)vuông góc với BC mà AC và KE cắt nhau tại D => D là trực tâm của tam giác KBC => BD vuoogn góc với KC ( 1 ) .M là trung điểm của KC => BM là đường cao đồng thời là đường trung trực của tam giác KBC ( 2 ) . từ ( 1 ) và ( 2 ) => B, D , M thằng hàng

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE
và AK=EC
nên BK=BC
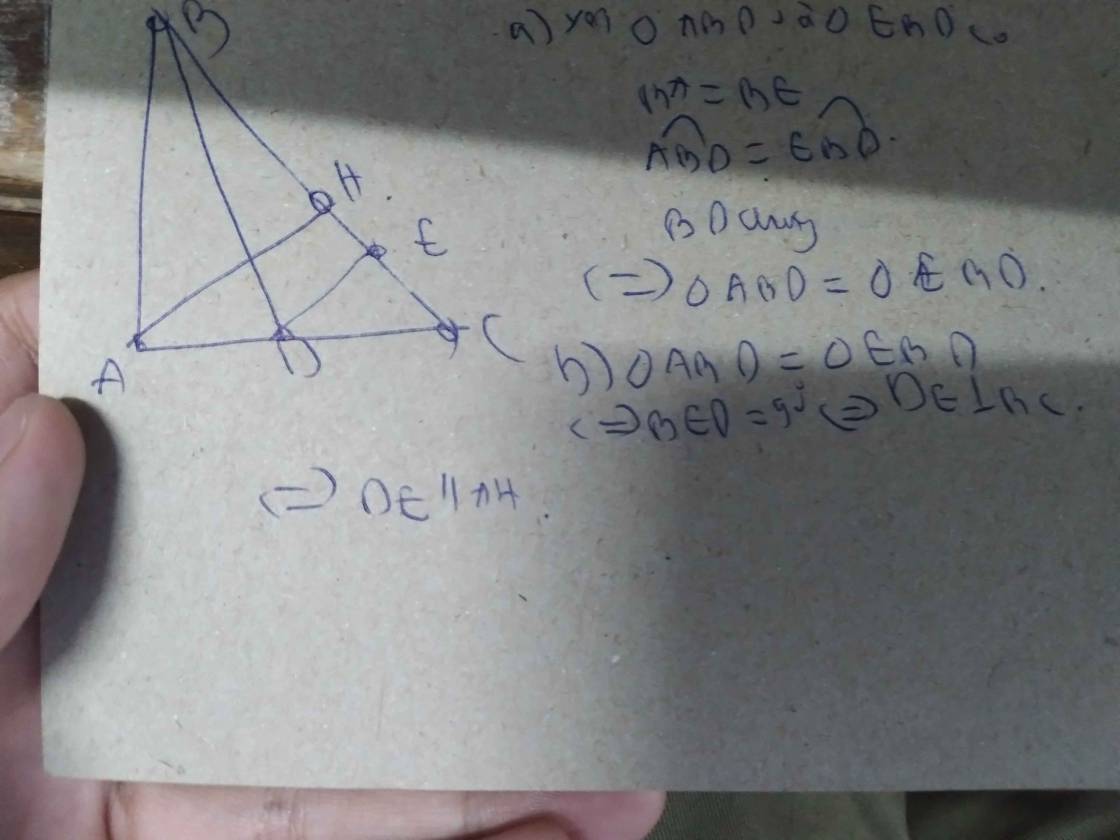
Để chứng minh các phần a), b), c), và d), chúng ta sẽ sử dụng các tính chất của tam giác vuông và các đường cao của tam giác.
a) Chứng minh tam giác ABD đều:
Vì tam giác ABC là tam giác vuông tại A và góc B = 60 độ, nên góc A = 90 - 60 = 30 độ.
Vì AH vuông BA và H là trung điểm của BD, nên AH cũng là đường cao của tam giác ABD.
Do đó, tam giác ABD có 1 cạnh là đường cao và 2 cạnh bằng nhau (AH = HD), nên tam giác ABD là tam giác đều.
b) Chứng minh D là trung điểm của BC:
Vì tam giác ABC là tam giác vuông tại A và góc B = 60 độ, nên góc A = 90 - 60 = 30 độ.
Vì AH vuông BA và H là trung điểm của BD, nên AH cũng là đường cao của tam giác ABD.
Do đó, tam giác ABD có 1 cạnh là đường cao và 2 cạnh bằng nhau (AH = HD), nên tam giác ABD là tam giác đều.
Vì tam giác ABD là tam giác đều, nên AD = BD.
Vì H là trung điểm của BD, nên AH = HD.
Vì AH vuông BA, nên tam giác AHB là tam giác vuông cân.
Vì góc AHB = 90 độ và góc A = 30 độ, nên góc HAB = 60 - 30 = 30 độ.
Vì góc HAB = góc AHB = 30 độ, nên tam giác AHB là tam giác đều.
Vì tam giác AHB là tam giác đều, nên BH = AB.
Vì BH = AB và AH = HD, nên tam giác BHD là tam giác đều.
Vì tam giác BHD là tam giác đều, nên BD = HD.
Vì AD = BD và BD = HD, nên AD = HD.
Vì H là trung điểm của BD, nên AD = HD = DH.
Vì AD = DH, nên D là trung điểm của AH.
Vì AH là đường cao của tam giác ABC, nên D là trung điểm của BC.
c) Chứng minh HE song song AB:
Vì tam giác ABC là tam giác vuông tại A và góc B = 60 độ, nên góc A = 90 - 60 = 30 độ.
Vì AH vuông BA và H là trung điểm của BD, nên AH cũng là đường cao của tam giác ABD.
Vì tam giác ABD là tam giác đều, nên góc ADB = 60 độ.
Vì góc ADB = góc ABD = 60 độ, nên tam giác ADB là tam giác cân.
Vì tam giác ADB là tam giác cân, nên AH là đường trung tuyến của tam giác ADB.
Vì H là trung điểm của BD, nên HE song song với đường trung tuyến AH.
Vì AH vuông BA, nên HE song song AB.