Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

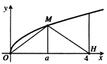
Chọn D
Tam giác ABC quay quanh trục là đường thẳng BC tạo ra hai khối nón:
-Khối nón đỉnh B, đường sinh BA.
-Khối nón đỉnh C, đường sinh CA.
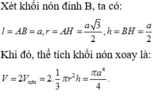

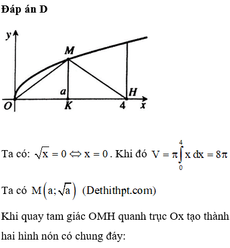
Đáp án A
Phương pháp:
Công thức tính thể tích khối nón: V = 1 3 S . h với S là diện tích hình tròn đáy và h là đường cao.
Cách giải:
Gọi A’ đối xứng với A qua BC. Khi quay tam giác quanh trục BC ta sẽ được hai khối nón có đáy là hình tròn tâm H bán kính R và lần lượt có chiều cao là BH và CH.
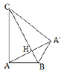
Ta có:
A C = B C 2 − A B 2 = 4 a 2 − a 2 = a 3
⇒ A H = A B . A C B C = a . a 3 2 a = a 3 2
V = 1 3 π A H 2 . B H + 1 3 π A H 2 . C H = 1 3 . π A H 2 . B C = 1 3 π a 3 2 2 .2 a = π a 3 2

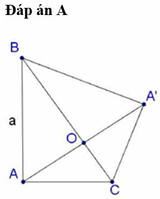
Đáp án B
Khi quay miền trong tam giác ABC quanh cạnh BC ta được hai hình nón, hình nón đỉnh B bán kính đáy OA, hình nón đỉnh C bán kính đáy OA.
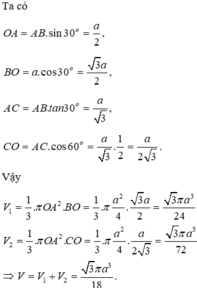

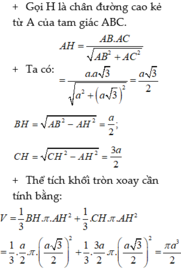




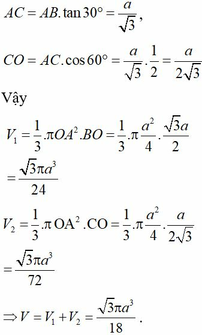
V = π a 3
Đáp án A