Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

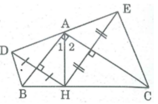
∆ ADB = ∆ AHB ⇒ BD = BH.
∆ AEC = ∆ AHC ⇒ CE = CH.
Vậy BD + CE = BH + CH = BC.

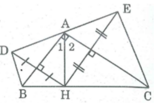
Điểm D đối xứng điểm H qua trục AB.
Suy ra AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực)
⇒ ∆ ADH cân tại A
Suy ra: AB là tia phân giác của ∠ (DAH)
⇒ ∠ (DAB) = ∠ A 1
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của góc (HAE) ⇒ ∠ A 2 = ∠ (EAC)
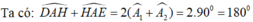
⇒ D, A, E thẳng hàng
Ta có: AD = AE (vì cùng bằng AH)
Suy ra điểm A là trung điểm của đoạn DE.
Vậy điểm D đối xứng với điểm E qua điểm A

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật

1: Ta có: D và H đối xứng nhau qua AB
nên AB là đường trung trực của DH
Suy ra: AH=AD
Xét ΔAHD có AH=AD
nên ΔAHD cân tại A
mà AB là đường trung trực ứng với cạnh đáy HD
nên AB là tia phân giác của \(\widehat{HAD}\)
Ta có: H và E đối xứng nhau qua AC
nên AC là đường trung trực của HE
Suy ra: AE=AH
Xét ΔAEH có AE=AH
nên ΔAEH cân tại A
mà AC là đường trung trực ứng với cạnh đáy HE
nên AC là tia phân giác của \(\widehat{EAH}\)
Ta có: \(\widehat{DAE}=\widehat{EAC}+\widehat{HAC}+\widehat{HAB}+\widehat{DAB}\)
\(=2\cdot\left(\widehat{HAC}+\widehat{HAB}\right)\)
\(=2\cdot90^0=180^0\)
Suy ra: D,A,E thẳng hàng
mà AE=AD(=AH)
nên A là trung điểm của DH
2: Ta có: DE=AD+AE
nên DE=AH+AH
hay DE=2AH

a: Xét tứ giác AHCD có
M là trung điểm chung của AC vàHD
góc AHC=90 độ
Do đó: AHCD là hình chữ nhật
b: Xét tứ giác ADHE có
AD//HE
AD=HE
Do đó: ADHE là hình bình hành