Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-30^0=60^0\)
Xét ΔBAM có BA=BM và \(\widehat{ABM}=60^0\)
nên ΔBAM đều
b: Ta có: ΔMAB đều
=>\(\widehat{MAB}=60^0\)
Ta có: \(\widehat{MAB}+\widehat{MAC}=\widehat{BAC}\)
=>\(\widehat{MAC}+60^0=90^0\)
=>\(\widehat{MAC}=30^0\)
Xét ΔMAC có \(\widehat{MAC}=\widehat{MCA}\left(=30^0\right)\)
nên ΔMAC cân tại M
=>MA=MC
mà MB=MA
nên MB=MC
=>M là trung điểm của BC
=>\(AM=MB=\dfrac{1}{2}BC\)
c: Ta có: ΔMAC cân tại M
mà MD là đường phân giác
nên MD\(\perp\)AC
Ta có: MD\(\perp\)AC
AB\(\perp\)AC
Do đó: MD//AB

xét ΔBAD và ΔBMD
có AB=BM
^ABD=^MBD
BD chnsg
suy ra ΔBAD =ΔBMD

ok, thanks nhưng dừng khoảng chừng là 2 giây, you lấy từ qanda

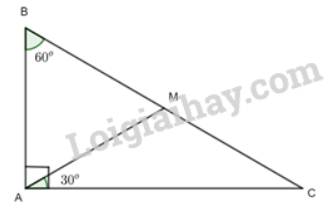
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
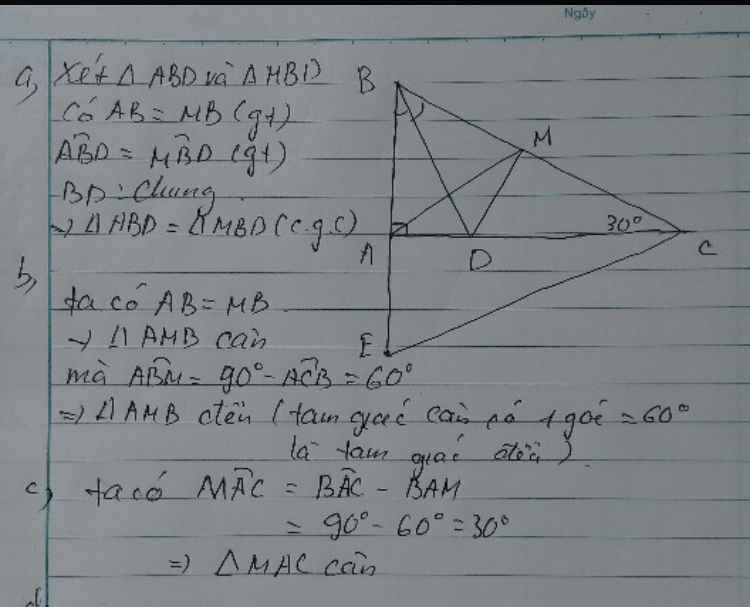
hình hơi xấu bạn nhé
ta có góc C = 30 độ nên
=> góc B = 60 độ (1)
ta lại có BM= BA
=> tam giác ABM là ta giác cân tại B (2)
từ (1) và (2) => tam giác ABM lả tam giác đều
b, ta có thể chứng minh tam giác AMC cân tại M ( vì có 2 góc kề đấy = nhau và = 30 độ )
=> MC = AM ( 1)
theo câu a ta có
ABM là tam giác đều nên AM = BM ( 2)
từ (1)và (2)
=> BM = MC mà BM + MC= BC
=> AM = BM = BC/2