Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔBAD có BA=BD và góc B=60 độ
nên ΔBAD đều
b: góc CAD=90-60=30 độ=góc C
=>ΔDAC cân tại D

a) Ta có:
\(BA=BD\rightarrow\Delta BAD\)cân tại \(B\)mà \(\widehat{ABD}=\widehat{B}=60^o\)
b) Ta có: \(\Delta BAD\)đều
\(\rightarrow\widehat{BAD}=60^o\)
\(\rightarrow=\widehat{DAC}=\widehat{BAC}-\widehat{BAD}=30^o\)
Lại có: \(\Delta ABC\)vuông tại \(A\rightarrow\widehat{ACB}=90^o-\widehat{ABC}=30^o\)
\(\rightarrow\widehat{DAC}=\widehat{ACB}=\widehat{ACD}\)
\(\rightarrow\Delta ADC\)cân tại \(D\)
c) Ta có: \(CA=CE\rightarrow\Delta CAE\)cân tại \(C\)
\(\rightarrow\widehat{EAC}=90^o-\frac{1}{2}\widehat{ACB}=90^o-\frac{1}{2}\widehat{ACB=75^o}\)
\(\rightarrow\widehat{DAE}=\widehat{CAE}-\widehat{CAD}=45^o\)
đccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi

a, ΔABD có BA = BD (gt) và ˆABDABD^ = ˆABCABC^ = 60o60o
⇒ ΔABD đều (đpcm)
b, ΔABD đều ⇒ AB = AD
Xét ΔAHB và ΔAHD có:
AH chung; AB = AD (cmt); HB = HD (H là trung điểm của BD)
⇒ ΔAHB = ΔAHD (c.c.c)
⇒ ˆAHBAHB^ = ˆAHDAHD^ mà 2 góc này kề bù
⇒ ˆAHBAHB^ = ˆAHDAHD^ = 90o90o
⇒ AH ⊥ BD (đpcm)
c, ΔABD đều ⇒ AB = BD = AD = 2cm
⇒ HB = HD = 1cm
⇒ HC = BC - HB = 5 - 1 = 4cm
ΔAHB vuông tại H ⇒ AH = √AB2−HB2AB2−HB2 = √22−1222−12 = √33cm
ΔAHC vuông tại H ⇒ AC = √AH2+HC2AH2+HC2 = √3+423+42 = √1919cm
a) Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Xét ΔBAD cân tại B có \(\widehat{ABD}=60^0\)(gt)
nên ΔBAD đều(Dấu hiệu nhận biết tam giác đều)
b) Ta có: ΔBAD đều(cmt)
mà AH là đường trung tuyến ứng với cạnh BD(gt)
nên AH là đường cao ứng với cạnh BD(Định lí tam giác cân)
hay AH\(\perp\)BD(Đpcm)
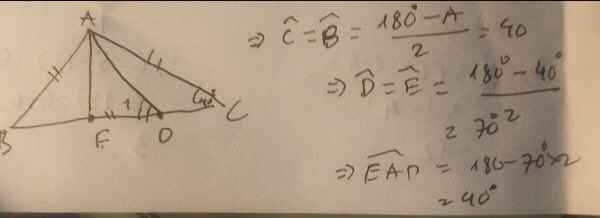
Bn Tùng Quân ơi vẽ hình ra giúp mk