Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có H nằm giữa B, C nên:
\(BC=BH+CH=10+42=52\left(cm\right)\)
Xét ΔABC vuông tại A và có đường cao AH ta có:
\(AB^2=BH\cdot BC\) (cạnh góc vuông và hình chiếu)
\(\Rightarrow AB=\sqrt{BH\cdot BC}\)
\(\Rightarrow AB=\sqrt{10\cdot52}=\sqrt{520}=2\sqrt{130}\left(cm\right)\)
Mà: \(\left|\overrightarrow{AB}\right|=AB\)
\(\Rightarrow\left|\overrightarrow{AB}\right|=2\sqrt{130}\left(cm\right)\)

AB^2=BH*BC
=>BH(BH+9)=20^2=400
=>BH^2+9BH-400=0
=>(BH+25)(BH-16)=0
=>BH=16cm
AH=căn BH*CH=12(cm)

a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
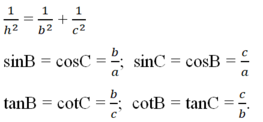

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE


Ta có tam giác EPQ cân tại E và CQ là phân giác góc BCA, nên E P Q ^ = E Q P ^ = H Q C ^ = 90 0 − H C Q ^ = 90 0 − P C K ^ .
Do đó E P Q ^ + P C K ^ = 90 0 , nên P K ⊥ A C .

a: Xét (O) có
góc BEC, góc BDC đều là các góc nội tiếp chắn nửa đường tròn
=>góc BEC=góc BDC=90 độ
=>CE vuông góc AB, BD vuông góc AC
Xét ΔABC có
CE,BD là đường cao
CE cắt BD tại H
=>H là trực tâm
=>AH vuông góc BC tại F
góc BEH+góc BFH=180 độ
=>BEHF nội tiếp
b: Xét ΔHCB có CO/CB=CM/CH
nên OM//BH
=>góc COM=góc CBH
=>góc COM=góc FEC
=>góc MOF+góc FEM=180 độ
=>OMEF nội tiếp

a: \(AH=\sqrt{BH\cdot CH}=6\left(cm\right)\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-\left(3\sqrt{13}\right)^2}=2\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{\sqrt{13}}\)
nên \(\widehat{B}=56^0\)
b: Xét ΔAHB vuông tại H và ΔCEH vuông tại E có
\(\widehat{BAH}=\widehat{C}\)
Do đó: ΔAHB\(\sim\)ΔCEH
Suy ra: \(\dfrac{AH}{CE}=\dfrac{BH}{EH}\)
hay \(AH\cdot HE=CE\cdot BH\)
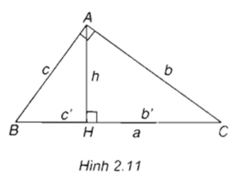
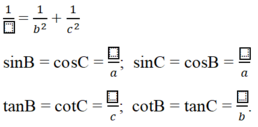
\(BC=BH+CH=25+144=169\left(cm\right)\)
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH có:
\(AH^2=HB.HC=25.144\Rightarrow AH=\sqrt{3600}=60\left(cm\right)\)
\(AB^2=BH.BC=25.169=4225\Rightarrow AB=\sqrt{4225}=65\left(cm\right)\)
\(AC^2=CH.CB=144.169=24336\Rightarrow AC=\sqrt{24336}=156\left(cm\right)\)