Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
b: Xét ΔBAC có
BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC tại F
Xét ΔBFH và ΔBDC có
góc BFH=góc BDC
góc FBH chung
=>ΔBFH đồng dạng với ΔBDC
=>BF/BD=BH/BC
=>BF*BC=BD*BH

a: Xét ΔEAC vuông tại A và ΔEDB vuông tại D có
\(\widehat{AEC}\) chung
Do đó: ΔEAC đồng dạng với ΔEDB
b: Ta có: ΔEDB vuông tại D
=>\(\widehat{DEB}+\widehat{DBE}=90^0\)
=>\(\widehat{DEB}=60^0\)
Xét ΔEDB vuông tại D có \(cosE=\dfrac{ED}{EB}\)
=>\(\dfrac{ED}{EB}=cos60=\dfrac{1}{2}\)
Ta có: ΔEAC đồng dạng với ΔEDB
=>\(\dfrac{EA}{ED}=\dfrac{EC}{EB}\)
=>\(\dfrac{EA}{EC}=\dfrac{ED}{EB}\)
Xét ΔEAD và ΔECB có
EA/EC=ED/EB
góc E chung
Do đó: ΔEAD đồng dạng với ΔECB
=>\(\dfrac{S_{EAD}}{S_{ECB}}=\left(\dfrac{ED}{EB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ECB}=50\cdot4=200\left(cm^2\right)\)

a: Xét ΔEAC vuông tại A và ΔEDB vuông tại D có
góc E chung
=>ΔEAC đồng dạng với ΔEDB
b: ΔEAC đồng dạng với ΔEDB
=>EA/ED=EC/EB
=>EA/EC=ED/EB
=>ΔEAD đồng dạng với ΔECB
=>S EAD/S ECB=(EA/EC)^2=1/4
=>S EBC=200cm2

a) -△DBE và △ACE có: \(\widehat{BDE}=\widehat{CAE};\widehat{BEC}\) là góc chung.
\(\Rightarrow\)△DBE∼△ACE (g-g).
b) △DBE∼△ACE \(\Rightarrow\dfrac{EB}{EC}=\dfrac{ED}{EA}\Rightarrow\dfrac{EB}{ED}=\dfrac{EC}{EA}\)
-△EAD và △ECB có: \(\dfrac{EB}{ED}=\dfrac{EC}{EA};\widehat{BEC}\) là góc chung.
\(\Rightarrow\)△EAD∼△ECB (c-g-c) nên \(\widehat{EAD}=\widehat{ECB}\)
c) EM cắt BC tại F.
-△BCE có: 2 đường cao BD và CA cắt nhau tại M.
\(\Rightarrow\)M là trực tâm của △BCE.
\(\Rightarrow\)EM⊥BC tại F.
-△BMF và △BCD có: \(\widehat{DBC}\) là góc chung, \(\widehat{BFM}=\widehat{BDC}=90^0\).
\(\Rightarrow\)△BMF∼△BCD (g-g).
\(\Rightarrow\dfrac{BM}{BC}=\dfrac{BF}{BD}\Rightarrow BM.BD=BC.BF\left(1\right)\)
-△CMF và △CBA có: \(\widehat{CFM}=\widehat{CAB}=90^0,\widehat{CBA}\) là góc chung.
\(\Rightarrow\)△CMF∼△CBA (g-g).
\(\Rightarrow\dfrac{CM}{CB}=\dfrac{CF}{CA}\Rightarrow CM.CA=CB.CF\left(2\right)\)
-Từ (1) và (2) suy ra:
\(BM.BD+CM.CA=BC.BF+CB.CF=BC\left(BF+CF\right)=BC.BC=BC^2\)
không đổi.

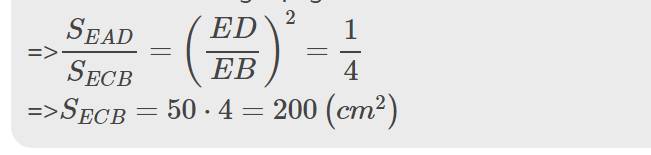
a: Xét ΔBHA và ΔBAC có
góc BHC=góc BAC
góc HBA chung
=>ΔBHA đồng dạng với ΔBAC
b: Xét ΔBHD vuông tại H và ΔBEC vuông tại E có
góc HBD chung
=>ΔBHD đồng dạng với ΔBEC
=>BH/BE=BD/BC
=>BH*BC=BE*BD=BA^2
c: BE*BD=BA*BA
=>BE/BA=BA/BD
=>ΔBEA đồng dạng với ΔBAD
=>góc BEA=góc BAD