M
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 12 2020
Hình vẽ bạn phải tự vẽ được chứ, bài này là bài rất rất rất cơ bản rồi đấy:vv
Ta có tam giác ABC là tam giác vuông
=> SABC=\(\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.4.3=6\) (cm2)
Áp dụng định lý Py-ta-go vào tam giác vuông ABC:
BC2=AB2+AC2=42+32=52
=> BC=5(cm)
Mà SABC=\(\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.AH.5=2,5.AH=6\)
=> AH=2,4(cm)
Vậy...
Có thể do cẩu thả mình sai số chỗ nào đó nhưng hướng làm như này nhé, đáng nhẽ bài này mình không giải đâu:vv
TU
13 tháng 3 2022
+xét tam giác ABC vuông tại A:
=> BC2=AC2+AB2(Định lý pytago)
hay BC2=16+9
BC2= 25
Mà BC>0
=> BC=5(cm)
+xét tam giác ABH vuông tại H và tam giác ABC vuông tại A có:
GÓC B: góc chung
góc A=góc H=90độ (tam giác ABC vuông tại A,AH:đường cao)
=> tam giác ABH đồng dạng với tam giác ABC(góc-góc)
=> BH/AB=BA/BC(các cặp cạnh tương ứng tỉ lệ)
hay BH/3=3/5
=> BH=1,8(cm)
=> HC=5-1,8=4,8(cm)
p/s: mình thấy sai sai , vì sao có dữ liệu phân giác góc C mà lại không dùng đến(bạn tham khảo thử bài mình thôi nhé).Các góc,đồng dạng,độ , bạn cùng kí hiệu.Thông cảm hình mình vẽ hơi tởm=))
13 tháng 9 2023
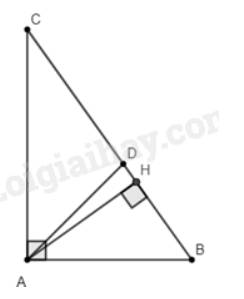
a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).
CM
7 tháng 9 2019
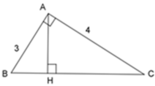
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 3 2 + 4 2 = B C 2
15 tháng 7 2021
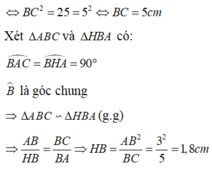
a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Ta có: ΔHBA\(\sim\)ΔABC(cmt)
nên \(\dfrac{BH}{BA}=\dfrac{BA}{BC}=\dfrac{AH}{CA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{BH}{3}=\dfrac{3}{5}=\dfrac{AH}{4}\)
Suy ra: BH=1,8cm; AH=2,4cm
9 tháng 5 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
MP
9 tháng 5 2023
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
CM
27 tháng 8 2018
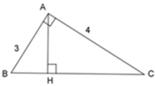
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 3 2 + 4 2 = B C 2
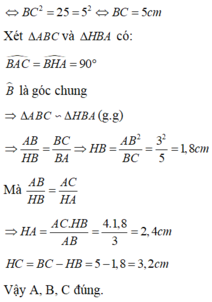
Đáp án: D
tớ chịu
Xét tam giác vuông HBA và tam giác vuông ABC có:
B là góc chung
suy ra tam giác vuông HBA đồng dạng tam giác vuông ABC
suy ra HB/AB=BA/BC=HA/AC
suy ra BA/BC=HA/AC
suy ra 3/5=HA/4(BC bạn tính theo Py- ta-go nhe)
suy ra HA=4x3/5=2,4cm