Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(BH=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
a: Đề sai rồi bạn
a.=> BC = BH + CH = 1 + 3 = 4 cm
áp dụng định lý pitago vào tam giác vuông AHB
\(AB^2=HB^2+AH^2\)
\(AB=\sqrt{1^2+2^2}=\sqrt{5}cm\)
áp dụng định lí pitago vào tam giác vuông AHC
\(AC^2=AH^2+HC^2\)
\(AC=\sqrt{2^2+3^2}=\sqrt{13}cm\)

a, Theo định lí Pytago tam giác ABH vuông tại H
\(AB=\sqrt{BH^2+AH^2}=\sqrt{5}cm\)
Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{4+9}=\sqrt{13}\)cm
-> BC = HB + HC = 4 cm
b, Ta có tam giacs ABC đều mà BH là đường cao hay BH đồng thời là đường trung tuyến
=> AH = AC/2 = 5/2
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=\dfrac{5\sqrt{3}}{2}cm\)

Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H, ta có:
AH²+BH²=AB²
AH²=AB²−BH²
AH²=52−32
⇒AH²=16
⇒AH=4(cm)
Ta có:
BH+HC=BC
⇒HC=BC−BH
⇒HC=8−3
⇒HC=5(cm)
Áp dụng định lí Py-ta-go vào tam giác AHC vuông tại H, ta có:
AH²+HC²=AC²
42+52=AC²
⇒AC²=41
⇒AC=√41(cm)
Vậy HC = 5 cm, AC = √41 cm
#Tuyên#

e: I là trực tâm của ΔBAD
=>DI vuông góc AB
=>DI//AC
=>góc BDI=góc ACB
DT là phân giác của góc IDB
=>góc TDI=góc TDB=1/2*góc BDI=1/2*góc ACB
DI//AC
=>góc IDA=góc DAC
AD là phân giác của góc HAC
=>góc DAC=1/2*góc HAC
=>góc IDA=1/2*góc HAC
góc HAC+góc ACB=90 độ
=>góc IDT+góc IDA=1/2*90=45 độ
=>góc TDA=45 độ
=>ΔTDA vuông cân

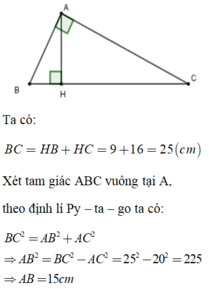
BC=25cm
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20cm