Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: BC=10cm
AH=4,8cm
c: Xét ΔABH vuông tại H có HM là đườg cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN\(\sim\)ΔACB
\(a)\) Xét \(\Delta ABC\) và \(\Delta HBA:\)
\(\widehat{BAC}=\widehat{BHA}\left(=90^o\right).\\ \widehat{ABC}chung.\\ \Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right).\)
\(b)\) Xét \(\Delta ABC\) vuông tại A:
\(+)BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=6^2+8^2=36+64=100.\\ \Rightarrow BC=10\left(cm\right).\)\(+)AH.BC=AB.AC\) (Hệ thức lượng).\(\Rightarrow AH.10=6.8.\\ \Rightarrow AH=4,8\left(cm\right).\)\(c)\) Xét \(\Delta ABH\) vuông tại H, đường cao MH:\(AH^2=AM.AB\) (Hệ thức lượng). \(\left(1\right)\)Xét \(\Delta ACH\) vuông tại H, đường cao NH:\(AH^2=AN.AC\) (Hệ thức lượng). \(\left(2\right)\)Từ \(\left(1\right);\left(2\right)\Rightarrow AM.AB=AN.AC.\)Xét \(\Delta ACB\) và \(\Delta AMN:\)\(\Rightarrow\dfrac{AB}{AN}=\dfrac{AC}{AM}.\)\(\widehat{A}chung.\\ \dfrac{AB}{AN}=\dfrac{AC}{AM}\left(cmt\right).\\ \Rightarrow\Delta ACB\sim\Delta AMN\left(c-g-c\right).\)
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
b: Xét tứ giác AHKC có
I là trung điểm chung của AK và HC
=>AHKC là hình bình hành
=>AC//KH
c: Ta có: AC//HK
AC//HM
HK,HM có điểm chung là H
Do đó: K,H,M thẳng hàng
Ta có: AMHN là hình chữ nhật
=>\(\widehat{NAH}=\widehat{NMH}\)
mà \(\widehat{NAH}=\widehat{CKH}\)(AHKC là hình bình hành)
nên \(\widehat{NMH}=\widehat{CKH}\)
Xét tứ giác MNCK có CN//MK
nên MNCK là hình thang
Hình thang MNCK có \(\widehat{CKM}=\widehat{NMK}\)
nên MNCK là hình thang cân
d: Ta có: AMHN là hình chữ nhật
=>AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Xét ΔCAH có
CO,AI là các đường trung tuyến
CO cắt AI tại D
Do đó: D là trọng tâm của ΔCAH
=>\(AD=\dfrac{2}{3}AI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AK=\dfrac{1}{3}AK\)
=>AK=3AD

a: BC=căn 6^2+8^2=10cm
AD là phân giác
=>BD/CD=AB/AC=3/4
=>BD/3=CD/4=(BD+CD)/(3+4)=10/7
=>BD=30/7cm
b: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA

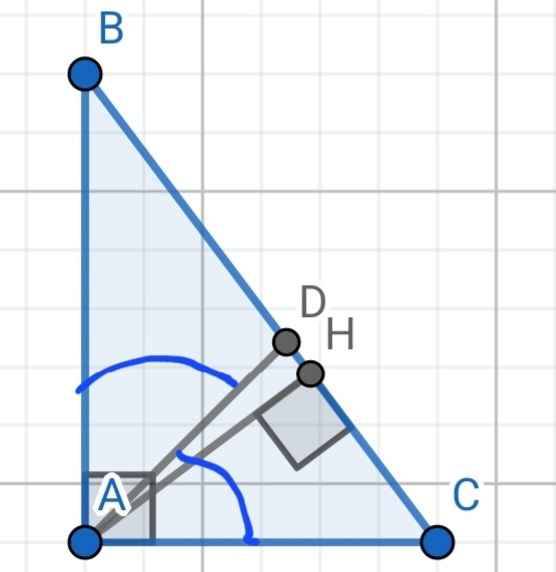
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA

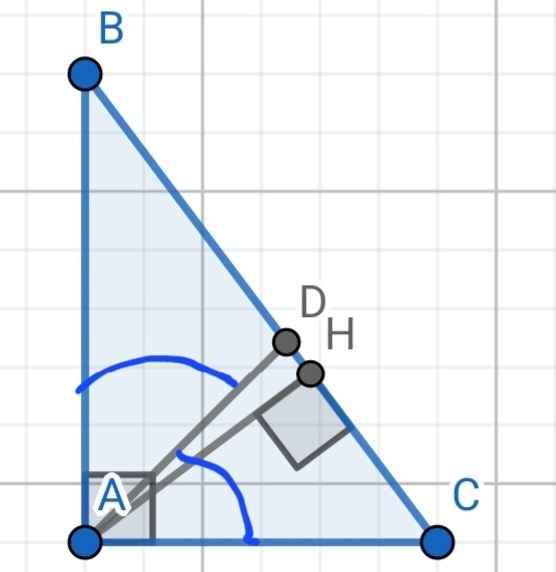
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
a: DB/DC=AB/AC=4/3
b: Sửa đề: AH/CA=AB/BC
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>AH*BC=AB*AC
=>AH/AC=AB/CB

a) Xét tứ giác AMHN có
\(\widehat{NAM}=90^0\)(\(\widehat{BAC}=90^0\), M∈AB, N∈AC)
\(\widehat{AMH}=90^0\)(HM⊥AB)
\(\widehat{ANH}=90^0\)(HN⊥AC)
Do đó: AMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)(1)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có AH là đường cao ứng với cạnh BC(gt)
nên \(S_{ABC}=\dfrac{AH\cdot BC}{2}=AH\cdot\dfrac{10}{2}=5\cdot AH\)(2)
Từ (1) và (2) suy ra \(5\cdot AH=24\)
hay AH=4,8cm
Ta có: AMHN là hình chữ nhật(cmt)
nên AH=MN(Hai đường chéo trong hình chữ nhật AMHN)
mà AH=4,8cm(cmt)
nên MN=4,8cm
Vậy: MN=4,8cm

a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
Vì AD là phân giác \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\Rightarrow\dfrac{CD}{AC}=\dfrac{BD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{CD}{AC}=\dfrac{BD}{AB}=\dfrac{BC}{AC+AB}=\dfrac{10}{14}=\dfrac{5}{7}\Rightarrow CD=\dfrac{40}{7}cm;BD=\dfrac{30}{7}cm\)
Xét tam giác ABH và tam giác CBA có
^AHB = ^BAC = 900
^ABH _ chung
Vậy tam giác ABH ~ tam giác CBA (g.g)
\(\dfrac{AB}{BC}=\dfrac{BH}{AB}\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)
-> DH = BD - BH = \(\dfrac{30}{7}-\dfrac{18}{5}=\dfrac{150-136}{35}=\dfrac{14}{35}=\dfrac{2}{5}\)cm
b, \(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}cm\)
Vì HM vuông AB; HN vuông AC ; BA vuông AC nên tg AMHN là hcn
=> AH = MN = 24/5 cm
c, Xét tam giác AHM và tam giác ABH có
^HAM _ chung ; ^AMH = ^AHB = 900
Vậy tam giác AHM ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AM}{AH}\Rightarrow AH^2=AM.AB\)
tương tự tam giác AHN ~ tam giác ACH (g.g)
\(\dfrac{AH}{AC}=\dfrac{AN}{AH}\Rightarrow AH^2=AN.AC\)
=> AM . AB = AN . AC
Câu c là AM. AB=AN. AC nha mn giúp mik vs