Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC

D) cách 2:
Xét∆BDC có: BA=AD
BM=MC
=) AM là đường trung bình của∆BCD
=) AM//DC
Mà: AE//MC ( gt )
Suy ra: * EC=AM. (1)
( t/c đường chắn)
* AE=MC . (2)
Lại có: ∆AEC cân tại E=) AE=EC (3)
Từ (1);(2);(3)=) AM = MC
Mà M là trung điểm BC=) MC=1/2BC
Suy ra AM=1/2BC

a, tam giác ABC vuông tại A (gt)
=> AB^2 + AC^2 = BC^2 (đl Pytago)
mà AB = 5; AC = 12
=> 5^2 + 12^2 = BC^2
=> BC^2 = 25 + 144
=> BC^2 = 169
=> BC = 13 do BC > 0
b, xét tam giác ABC và tam giác ADC có : AC chung
AB = AD (gt)
góc BAC = góc DAC = 90
=> tam giác ABC = tam giác ADC (2cgv)
c, AE // BC (gt)
=> góc AEC = góc ACB (slt)
mà góc ACB = góc ACD do tam giác ABC = tam giác ADC (Câu a)
=> góc EAC = góc ACD (tcbc)
=> tam giác ACE cân tại E (tc)
d, cm E là trung điểm của DC
a) Áp dụng định lý Py - ta - go vào tam giác ABC vuông tại A, ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Leftrightarrow BC=\sqrt{5^2+12^2}\)
\(\Leftrightarrow BC=\sqrt{25+144}\)
\(\Leftrightarrow BC=\sqrt{169}\)
\(\Leftrightarrow BC=13\)
Vậy BC = 13cm

b) Xét ΔABC vuông tại A và ΔADC vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔABC=ΔADC(hai cạnh góc vuông)
a) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13(cm)
Vậy: BC=13cm

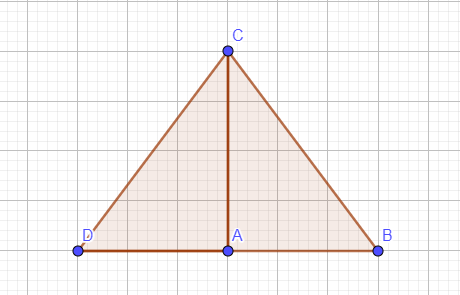
`a)` Áp dụng định lý pytago ta có :
`AB^2+AC^2=BC^2`
hay `9^2+12^2=BC^2`
`=>BC^2=225`
`=>BC=15(cm)`
`b)` Xét `ΔABC` và `ΔADC` ta có :
`AC` chung
`\hat{BAC}=90^o`
`\hat{DAC}=90^o`
`=>ΔABC=ΔADC` (c.g.c)

a) Áp dụng định lý Py-ta-go cho \(\Delta\)vuông ABC có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+12^2}=13\left(cm\right)\)
b) Xét \(\Delta ABC\)và \(\Delta ADC\)có:
\(\hept{\begin{cases}AB=AD\left(gt\right)\\gócBAC=gócDAC\left(=90^0\right)\\AC:chung\end{cases}}\)
\(\Rightarrow\Delta ABC=\Delta ADC\left(c.g.c\right)-\left(đpcm\right)\)
c) Xét \(\Delta BDC\)có: \(\hept{\begin{cases}\text{A là trung điểm BD}\\AE//BC\left(gt\right)\end{cases}}\)
\(\Rightarrow\text{E là trung điểm CD}\left(t/c\right)\)
Xét \(\Delta ADC\)vuông tại A có AE là đường trung tuyến ứng cạnh DC
\(\Rightarrow AE=\frac{1}{2}CD\left(t/c\right)=EC\left(\text{E là trung điểm CD}\right)\)
\(\Rightarrow\Delta AEC\)cân tại E (đpcm)
d) Gọi giao của AC và BE là O
Xét \(\Delta DBC\)có:\(\hept{\begin{cases}\text{BE là đường trung tuyến ứng cạnh CD }\left(gt\right)\\\text{CA là đường trung tuyến ứng cạnh BD }\left(gt\right)\end{cases}}\)
\(\Rightarrow\)O là trọng tâm của \(\Delta DBC\)
Mà DF là đường trung tuyến ứng cạnh BC
\(\Rightarrow\)CA, DF, BE cùng đồng quy tại 1 điểm (đpcm)

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng

Á dụng định lý yTaGo vào tam giác vuông ABC ta có
BC2=AC2+AB2
BC2=122+52
BC2=169
Ý b
Xét tam giác ABC và tam giác ADC
góc CAB= góc CAD
AC chung
AB=AD
Vậy tam giác ABC= tam giác ADC(c.g.c)
ý c
Vì tam giác ABC= tam giác ADC(cmt)
suy ra góc ACD= góc ACB
mà AE song song với BC
suy ra góc EAC= góc ACB(hai góc sole trong)
mà góc ACD= góc ACB
vậy tam giác RAC cân tại E
ý d
gọi gia điểm của DF,CA,BE là I
Có FB=FC(F là trung điểm của BC)
AB=AD (gt)
suy ra DF và AC là hai đường trung tuyến của tam giác BDC
mà hai đường này cắt nhau tại I
suy ra I là trọng tâm của tam giác BDC
suy ra BE là đường trung tuyến còn lại
Vậy DF,CA,BE đồng quy tại 1 điểm
a) Áp dụng định lí Py-ta-go vào \(\Delta ABC\)vuông tại A , ta được :
AB2 + AC2 = BC2
\(\Rightarrow\)BC2 = 52 + 122 = 132
\(\Rightarrow\)BC = 13
b) Xét \(\Delta ABC\)và \(\Delta ADC\)có :
AB = AD ( gt )
\(\widehat{BAC}=\widehat{DAC}=90^o\)
AC ( cạnh chung )
Suy ra : \(\Delta ABC\)= \(\Delta ADC\)( c.g.c )
\(\Rightarrow\)\(\widehat{DCA}=\widehat{BCA}\); \(\widehat{ADC}=\widehat{ABC}\); DC = BC
c) vì AE // BC nên \(\widehat{EAC}=\widehat{BCA}\)
Suy ra : \(\widehat{EAC}=\widehat{DCA}\)
\(\Rightarrow\)\(\Delta EAC\)cân tại E
\(\Rightarrow\)AE = EC
d) Gọi giao điểm của BE và AC là H
vì AE // BC nên \(\widehat{DAE}=\widehat{ABC}\)
\(\Rightarrow\)\(\widehat{DAE}=\widehat{ADE}\)
\(\Rightarrow\)\(\Delta DAE\)cân tại E
\(\Rightarrow\)DE = AE
\(\Rightarrow\)AE = \(\frac{1}{2}DC=\frac{1}{2}BC\)
Ta có : BE + AC = ( BH + HC ) + ( AH + HE ) > BC + AE = BC + \(\frac{1}{2}BC\)= \(\frac{3}{2}BC\)