Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Khi quay tam giác BMC quanh cạnh AB tạo ra 2 khối tròn xoay có thể tích là
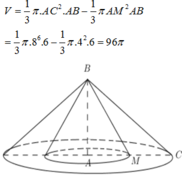

Đáp án D
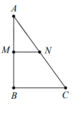
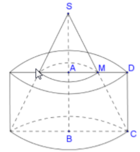
Xét khối nón tròn xoay ( N 1 ) được tạo thành khi quay tam giác AMN quanh trục A B ⇒ N 1 có bán kính đáy r 1 = M N = 2 ; chiều cao h 1 = A M = 5 . Suy ra thể tích khối nón ( N 1 ) là V 1 = 1 3 πr 1 2 h = 1 3 π . 2 2 . 5 = 20 π 3 .
Xét khối nón tròn xoay N 2 được tạo thành khi quay tam giác ABC
quanh trục A B ⇒ N 2 có bán kính đáy r 2 = B C = 4 ; chiều cao h 2 = A B = 10 .
Suy ra thể tích khối nón N 2 là V 2 = 1 3 πr 2 2 h 2 = 1 3 π . 4 2 . 10 = 160 π 3 .
Vậy thể tích khối tròn xoay cần tính là V = V 1 - V 2 = 160 π 3 - 20 π 3 = 140 π 3 .

Chọn đáp án C.
Chuẩn hóa BC = 5; AC = 4; AB = 3 →∆ABC vuông tại A.
Khi quay ∆ABC quanh AC, ta được khối nón N 1 có bán kính đáy r = AB = 3, độ dài đường sinh l = BC = 5 suy ra diện tích toàn phần của N 1 là S b = 24 π
Khi quay ∆ABC quanh AB, ta được khối nón N 2 có bán kính đáy r = AC = 4, độ dài đường sinh l = BC = 5 suy ra diện tích toàn phần của N 2 là S c = 36 π
Khi quay ∆ABC quanh BC, ta được khối nón N 3 , N 4 có bán kính đáy là chiều cao của tam giác ABC và bằng 12/5, độ dài đường sinh lần lượt là 3,4 suy ra diện tích toàn phần của khối tròn xoay S a = S 3 + S 4 = 708 π 25
Vậy S C > S a > S b

Đáp án D
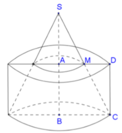
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
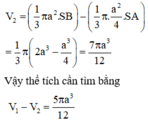

Đáp án A
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích

Đáp án C
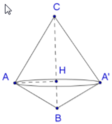
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ΔABC, gọi H là chân đường cao của A đến BC. Ta có


Đáp án C
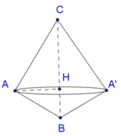
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ∆ A B C , gọi là H chân đường cao của A đến BC. Ta có


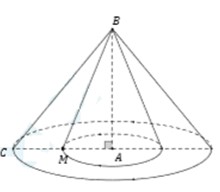

Đáp án C