Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\widehat{ABC}=60^o\)( theo đề bài )
\(b,\)Xét \(\Delta ABD\)và \(\Delta HBD\)có :
\(BD\)là cạnh chung \(\left(1\right)\)
\(\widehat{B1}=\widehat{B2}=30^o\)( do \(BD\)là tia phân giác của \(\widehat{ABC}\)) \(\left(2\right)\)
Ta có : \(\widehat{D1}=180^o-\widehat{B1}-\widehat{A}\)
\(=180^o-30^o-90^o=60^o\)
\(\widehat{D2}=180^o-\widehat{B2}-\widehat{H1}\)
\(=180^o-30^o-90^o=60^o\)
\(\Rightarrow\widehat{D1}=\widehat{D2}\)\(\left(3\right)\)
Từ : \(\left(1\right);\left(2\right);\left(3\right)\)suy ra : \(\Delta ABD=\Delta HBD\left(g.c.g\right)\)
\(c,\)Không có điểm \(K\)


a) Xét ΔABD vuông tại A và ΔHBD vuông tại H có:
- BD là cạnh chung
- \(\widehat{ABD}=\widehat{HBD}\) (vì BD là tia phân giác \(\widehat{ABC}\))
Suy ra ΔABD = ΔHBD (cạnh huyền - góc nhọn)
b) Từ a) suy ra AD = DH (hai cạnh tương ứng)
c) Đề bị thiếu: Điểm M ở đâu???
a) + Vì tam giác ABC vuông tại A (gt)
=> tam giác ABD vuông tại a
+ Vì DH vuông góc với BC (gt)
=> tam giác HBD vuông tại H
+ Xét ΔABD và ΔHBD, có:
+ Chung BD
+ góc ABD = góc HBD (BD là tia phân giác của góc ABC)
=> ΔABD = ΔHBD (cạnh huyền - góc nhọn)
b) Vì ΔABD = ΔHBD (cmt)
=> AD = DH (2 cạnh tương ứng)
c) Ko đủ dữ kiện

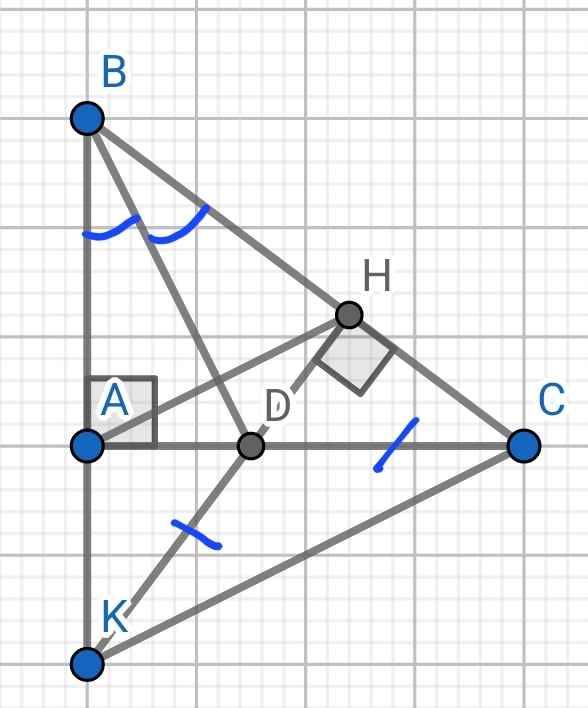
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng

a: \(\widehat{ACB}=30^0\)
b: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AD=AC
AB chung
Do đó: ΔABD=ΔABC

1) Chứng minh: ΔABD = ΔEBD
Xét ΔABD và ΔEBD, có:
BD là cạnh huyền chung (gt)
Vậy ΔABD = ΔEBD (cạnh huyền – góc nhọn)
2) Chứng minh: ΔABE là tam giác đều.
ΔABD = ΔEBD (cmt)
AB = BE
mà góc B = 60 độ (gt)
Vậy ΔABE có AB = BE và góc 60 độ nên ΔABE đều.
3) Tính độ dài cạnh BC
Ta có (gt)
Góc C+B = 90 độ(ΔABC vuông tại A)
Mà BEA = góc B = 60 độ (ΔABE đều)
Nên góc EAC = góc C ΔAEC cân tại E
EA = EC mà EA = AB = EB = 5cm
Do đó EC = 5cm
Vậy BC = EB + EC = 5cm + 5cm = 10cm

a: Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔBAD=ΔBHD

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
DO đó: ΔBAD=ΔBED
Suy ra: BA=BE
hay ΔBAE cân tại B


a) tính góc ABC