Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
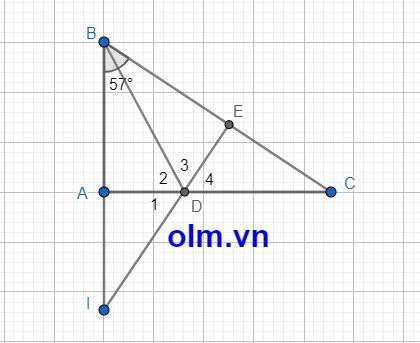
Xét tam giác ABD và tam giác EBD có
\(\widehat{ABD}\) = \(\widehat{EBD}\) (gt)
AB = BE (gt)
BD chung
⇒\(\Delta\)ABD = \(\Delta\) EBD (c-g-c)
⇒AD = DE
⇒ \(\widehat{BAD}\) = \(\widehat{BED}\) = 900
\(\widehat{DEC}\) = 1800 - 900 = 900
Xét tam giác ADI và tam giác EDC có:
\(\widehat{DAI}\) = \(\widehat{DEC}\) = 900 (cmt)
AD = DE (cmt)
AI = EC (gt)
⇒ \(\Delta\)ADI = \(\Delta\)EDC (c-g-c)
⇒ D1 = D4
Mà D2 + D3 + D4 = 1800
⇒ D1 + D2 + D3 = 1800
⇒ \(\widehat{IDE}\) = 1800
⇒ I;D;E thẳng hàng (đpcm)
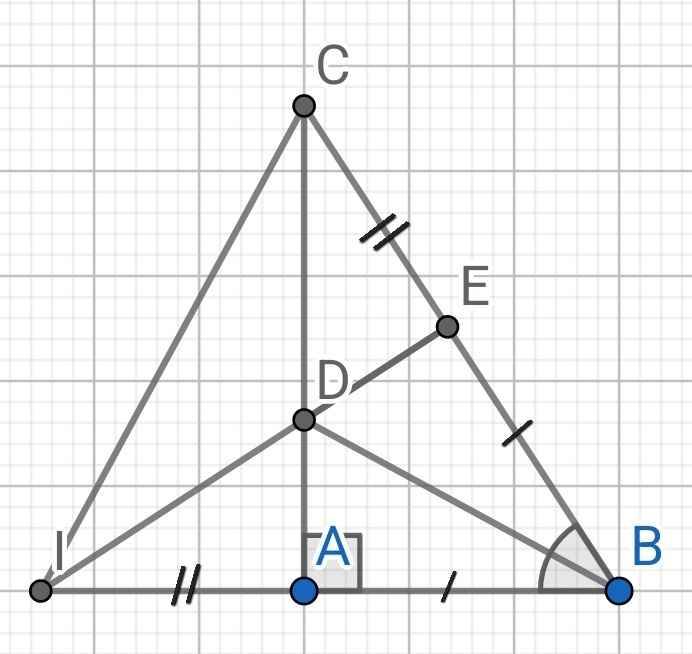Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ DE ⊥ BC
Do AI = EC (gt)
AB = BE (gt)
⇒ BI = AI + AB = BE + EC = BC
∆BCI có:
BI = BC (cmt)
⇒ ∆BCI cân tại B
Mà BD là tia phân giác của ∠ABC
⇒ BD là tia phân giác của ∠IBC
⇒ BD là đường cao của ∆BCI
Lại có:
CA ⊥ AB (∆ABC vuông tại A)
CA ⊥ BI
⇒ CA là đường cao thứ hai của ∆BCI
⇒ ID là đường cao thứ ba của ∆BCI
⇒ ID ⊥ BC
Mà DE ⊥ BC (cmt)
⇒ I, D, E thẳng hàng
a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: DA=DM
=>góc DAM=góc DMA
Câu a và câu b tham khảo tại link: Câu hỏi của Aftery - Toán lớp 7 - Học toán với OnlineMath
c) Xét \(\Delta\)ABE có AH vuông góc với AE và; HA = HE
=> AH là đường cao đồng thời là đường trung tuyến của \(\Delta\)ABE
=> \(\Delta\)ABE cân tại B
=> AB = BE
d) Ta có: SN vuông AH ; BC vuông AH
=> SN //BC
=> NK //MC
=> ^KNI = ^MCI
mặt khác có: NK = MC ; IN = IC ( gt)
=> \(\Delta\)NIK = \(\Delta\)CIM
=> ^NIK = ^CIM mà ^NIK + ^KIC = 180o
=> ^CIM + ^KIC = 180o
=> ^KIM = 180o
=>M; I ; K thẳng hàng
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%226.5%22%20y%3D%2216%22%3ED%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2217.5%22%20y%3D%2216%22%3EK%3C%2Ftext%3E%3Ctext%20font-family%3D%22math11ce3e6e3f452828e23a0c94572%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2232.5%22%20y%3D%2216%22%3E%26%23x22A5%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2246.5%22%20y%3D%2216%22%3EB%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2258.5%22%20y%3D%2216%22%3EC%3C%2Ftext%3E%3C%2Fsvg%3E)
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2216%22%3EB%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2213.5%22%20y%3D%2216%22%3EI%3C%2Ftext%3E%3Ctext%20font-family%3D%22math11ce3e6e3f452828e23a0c94572%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2224.5%22%20y%3D%2216%22%3E%26%23x22A5%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2238.5%22%20y%3D%2216%22%3EE%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2250.5%22%20y%3D%2216%22%3EC%3C%2Ftext%3E%3C%2Fsvg%3E)
a: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)
hay DK\(\perp\)BC
b: Xét ΔBEC có BE=BC
nên ΔBEC cân tại B
mà BI là đường phân giác
nên BI là đường cao
Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)