Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAC co BM/BA=BN/BC
nên MN//AC và MN=AC/2
=>AMNC là hình thang
mà góc MAC=90 độ
nen AMNC là hình thang vuông
b: Xét tứ giác ANBH có
M là trung điểm chung của AB và NH
NA=NB
nên ANBH là hình thoi

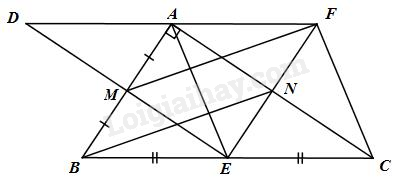
a) \(N\), \(E\) lần lượt là trung điểm của \(AC\) và \(BC(gt)\); Suy ra \(NE\) là đường trung bình của tam giác \(ABC\).
Suy ra \(NE\) // \(AB\)
Suy ra tứ giác \(ANEB\) là hình thang.
Mà \(\widehat {NAB} = 90^\circ \) (do \(\Delta ABC\) vuông tại \(A\))
Do đó tứ giác \(ANEB\) là hình thang vuông.
b) \(M\), \(E\) lần lượt là trung điểm của \(AB\) và \(BC\) (gt);
Suy ra \(ME\) là đường trung bình của \(\Delta ABC\)
Suy ra \(ME\) // \(AC\) hay \(ME\) // \(AN\)
Mà \(AM\) // \(NE\) (do \(AB\) // \(NE\))
Suy ra tứ giác \(AMEN\) là hình bình hành
Mà \(\widehat {{\rm{MAN}}} = 90^\circ \) nên \(AMEN\) là hình chữ nhật
c) Xét tứ giác \(BMFN\) có: \(MF\) // \(BN\) (gt) và \(BM\) // \(FN\) (do \(AB\) // \(NE\))
Suy ra \(BMFN\) là hình bình hành
Suy ra \(BM = FN\)
Mặt khác \(NE = AM\) (Tứ giác \(ANEM\) là hình chữ nhật) và \(AM = BM\)
Suy ra \(FN = NE\)
Tứ giác \(AFCE\) có \(N\) là trung điểm của \(AC\) và \(EF\)
Suy ra \(AFCE\) là hình bình hành
Mà \(AC \bot EF\)
Do đó \(AFCE\) là hình thoi
d) Xét tứ giác \(ADBE\) ta có: \(DE\) và \(AB\) cắt nhau tại \(M\) (gt)
Mà \(M\) là trung điểm của \(AB\) (gt)
\(M\) là trung điểm của \(DE\) (do \(D\) đối xứng với \(E\) qua \(M\))
Suy ra \(ADBE\) là hình bình hành
Suy ra \(AD\) // \(BE\) hay \(AD\) // \(EC\)
Mà \(AF\) // \(EC\) (do \(AECF\) là hình thoi)
Suy ra \(A,D,F\) thẳng hàng (1)
Mà \(ADBE\) là hình bình hành
Suy ra \(BE\) // \(AD\)
Mà \(AF = EC\) (do \(AFCE\) là hình thoi); \(EB = EC\) (gt)
Suy ra \(AD = AF\)(2)
Từ (1) và (2) suy ra \(A\) là trung điểm của \(DF\)

a: Xét ΔABC có
M là trung điểm của BC
E là trung điểm của AC
Do đó: ME là đường trung bình
=>ME//AB và ME=AB/2
hay ME//AH và ME=AH
Xét tứ giác AEMB có ME//AB
nên AEMB là hình thang
mà \(\widehat{EAB}=90^0\)
nên AEMB là hình thang vuông
b: Xét tứ giác MHAE có
ME//AH
ME=AH
Do đó: MHAE là hình bình hành
mà \(\widehat{HAE}=90^0\)
nên MHAE là hình chữ nhật
c: Xét tứ giác BHEM có
ME//BH
ME=BH
Do đó: BHEM là hình bình hành
d: Xét tứ giác BFAM có
H là trung điểm của AB
H là trung điểm của MF
Do đó: BFAM là hình bình hành
mà MA=MB
nên BFAM là hình thoi

a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC hay BMNC là hình thang

a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A
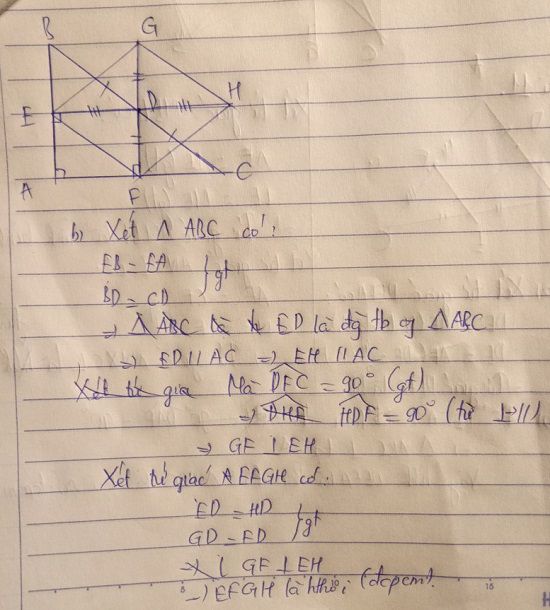

a: Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//AB
Xét tứ giác ANMB có MN//AB
nên ANMB là hình thang
mà \(\widehat{NAB}=90^0\)
nên ANMB là hình thang vuông
b: Xét tứ giác AMCD có
N là trung điểm của AC
N là trung điểm của MD
Do đó; AMCD là hình bình hành
mà MA=MC
nên AMCD là hình thoi