Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét t.g ABC có I là trung điểmBC ; IN // AB (cùng vuông góc vs AC)=> N là trung điểm AC
Xét tứ giác ADCI có
N là trđ AC
N là trđ DI
\(\widehat{ANI}=90^o\)
AC cắt DI tại N
=> ADCI là hình htoi
b/ Gọi O là giao điểm AI và BN
=> O là trọng tâm t/g ABC
=> OI = 1/3 AI = 1/2 DCt/g OIN= t/gKDN (g.c.g)
=> KD = IO = 1/3DC=> ĐPcm
c/ Theo Pythagoras ; AC = 16 cm
Cí IN = 1/2 AB ; IN = 1/2 ID=> ID = AB = 12
Có \(S_{ADCI}=\dfrac{1}{2}.ID.AC=8.12=96\left(cm^2\right)\)

a) Chứng minh được ADCI là hình thoi.
b) Gọi AI Ç BN = G Þ là trọng tâm DABC.
Ta chứng minh DK = GI, lại có D C = A I ⇒ D K D C = G I A I = 1 3
c) SADCI = 2SACI = SABC = 96cm2

a: Xét ΔABC có
I là trung điểm của CB
IN//AB
=>N là trung điểm của AC
Xét tứ giác AICD có
N là trung điểm chung của AC và ID
IA=IC
=>AICD la hình thoi
c: \(AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
IN=AB/2=6cm
=>DI=12cm
\(S_{ADCI}=\dfrac{1}{2}\cdot12\cdot16=8\cdot12=96\left(cm^2\right)\)

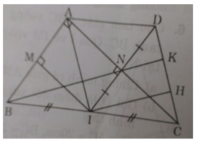
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.