Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tg vuông ABC có
BM=CM (gt) => AM=BM=CM=BC/2 (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
=> tg ABM cân tại M => \(\widehat{BAM}=\widehat{ABM}\) (góc ở đáy tg cân)
b/ Xét tg vuông AEF và tg vuông AFM có
\(\widehat{AEF}=\widehat{FAM}\) (cùng phụ với \(\widehat{AFE}\) ) (1)
Mà AM=CM (cmt) => tg MAC cân tại M => \(\widehat{FAM}=\widehat{ACB}\) (góc ở đáy th cân) (2)
Từ (1) và (2) \(\Rightarrow\widehat{ACB}=\widehat{AEF}\)
Xét tg MBE và tg MFC có
\(\widehat{AEF}=\widehat{ACB}\) (cmt)
\(\widehat{BME}=\widehat{CMF}\) (góc đối đỉnh)
=> tg MBE đồng dạng với tg MFC (g.g.g)
c/ Xét tg vuông ABC và tg vuông AFE có
\(\widehat{AEF}=\widehat{ACB}\) (cmt)
=> tg ABC đông dạng với tg AFE
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\Rightarrow AB.AE=AC.AF\)
d/

a: Xét ΔBAD vuông tại A và ΔBHA vuông tại H có
góc ABD chung
=>ΔBAD đồng dạng với ΔBHA
=>BA/BH=BD/BA
=>BA^2=BH*BD
b: Xét ΔAMB có IE//MB
nên IE/MB=AI/AM
Xét ΔAMC có ID//MC
nên ID/MC=AI/AM
=>IE/MB=ID/MC
mà MB=MC
nên IE=ID
=>I là trung điểm của ED
c: DE//BC
=>DI/BM=HI/HM
=>EI/CM=HI/HM
mà góc EIH=góc HMC
nên ΔIEH đồng dạng với ΔMCH
=>góc IHE=góc MHC
=>C,H,E thẳng hàng

a: Xét ΔAHB vuông tại H và ΔCHA vuôg tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
MH/MC=AH/AC=HB/AB
b: Xét ΔABE và ΔCMA có
góc BAE=góc MCA
góc ABE=góc CMA
=>ΔABE đồng dạng vơi ΔCMA
=>góc AEB=góc CAM
=>góc BEA=góc EAM
=>AM//BE

Câu b. Từ H kẻ đường thẳng song song AC cắt EM tại K
Ta chứng minh được BH/BM=EH/EA =>đpcm
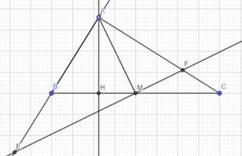

a: ΔABC vuông tại A
mà AM là trung tuyến
nên AM=MB=MC
=>góc MBA=góc MAB
b: góc AEF=90 độ-góc EAM=90 độ-góc B
=>gócAEF=góc ACB
c: Xét ΔAFE vuông tại A và ΔABC vuông tại A có
góc AEF=góc ACB
=>ΔAFE đồng dạng với ΔABC
=>AF/AB=AE/AC
=>AF*AC=AB*AE