Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

b) Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔABH\(\sim\)ΔCBA(g-g)
Suy ra: \(\dfrac{AB}{CB}=\dfrac{HB}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BC\cdot BH\)(đpcm)
Có gấp thế nào đi nữa thì phải đủ dữ kiện đề tụi tớ mới giúp được cậu nhé :))

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)
=>\(\dfrac{DA}{6}=\dfrac{DC}{10}\)
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà DA+DC=AC=8cm(D nằm giữa A và C)
nên \(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{8}{8}=1\)
=>\(DA=3\cdot1=3cm;DC=5\cdot1=5cm\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}=5\left(cm\right)\)
mà DC=5cm
nên CM=CD
Xét ΔCDI và ΔCMI có
CD=CM
\(\widehat{DCI}=\widehat{MCI}\)
CI chung
Do đó: ΔCDI=ΔCMI
=>\(\widehat{CID}=\widehat{CIM}\) và \(\widehat{IMC}=\widehat{IDC}\)(3)
Ta có: \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}\)(góc IDC là góc ngoài tại đỉnh D của ΔABD)
nên \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}=90^0+\widehat{ABD}\)(2)
Xét ΔBIM có \(\widehat{IMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{IMC}=\widehat{MIB}+\widehat{MBI}\left(1\right)\)
Từ (1),(2),(3) suy ra \(\widehat{MIB}+\widehat{MBI}=90^0+\widehat{ABD}\)
mà \(\widehat{MBI}=\widehat{ABD}\)
nên \(\widehat{MIB}=90^0\)

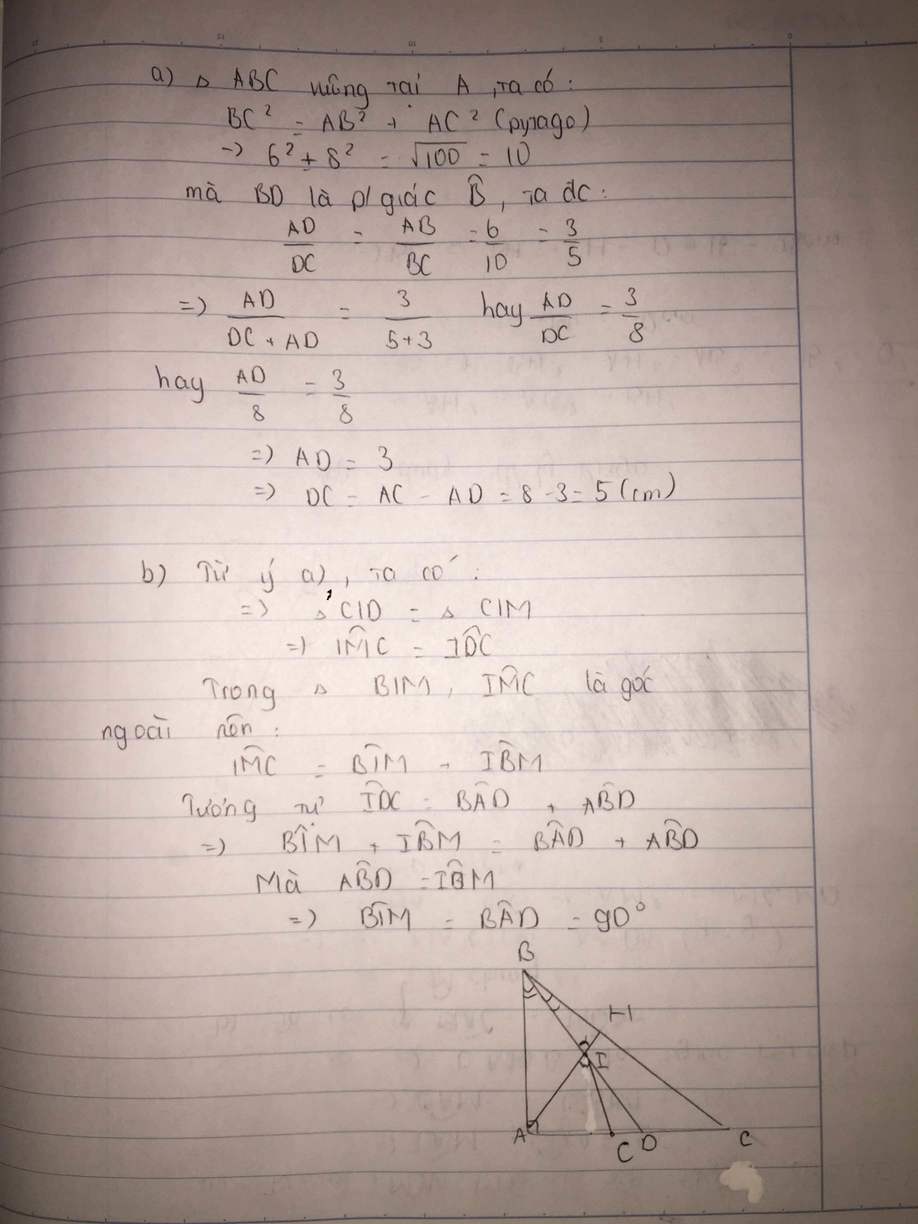
a)Xét △ABC vuông tại A có
BC2 = AB2 + AC2 (Py-ta-go)
BC2 = 62 + 82
BC2 = 36 + 64
BC2 = 100
=> BC = 10cm
Xét △ABC có:
BD là tia phân giác
=> \(\frac{AD}{DC}\)=\(\frac{AB}{BC}\) (t/c tia phân giác)
hay \(\frac{AD}{AD+DC}\)=\(\frac{6}{BC+AB}\)
=>\(\frac{AD}{AC}\)=\(\frac{6}{10+6}\)
=>\(\frac{AD}{8}\)=\(\frac{6}{16}\)
=>AD = \(\frac{8.6}{16}\) = 3cm
mà AC=8cm => DC = AC - AD = 8 - 3 = 5cm
b)xét △ABC vuông tại A có :
SABC = \(\frac{1}{2}\)AB.AC
SABC = \(\frac{1}{2}\)AH.BC
=> \(\frac{1}{2}\)AB.AC = \(\frac{1}{2}\)AH.BC
=>AB.AC = AH.BC
hay 6.8 = AH.10
=> 48 = AH.10
=>AH = \(\frac{48}{10}\)=4,8cm
Xét △AHC vuông tại H có :
AC2 = AH2 + HC2 (Py-ta-go)
hay 82 = 4,82 + HC2
=> HC2 = 64 - 23,04
=>HC2 = 40,96
=>HC = 6,4cm
c) Vì BC = 10cm (cmt)
mà M là trung điểm của BC
=> MB = MC = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)10 = 5cm
Mà DC = 5cm (cmt)
=> MC = DC
Xét △MCI và △DCI có
CI chung
góc DCI = góc MCI (do CI là tia phân giác)
MC = DC (cmt)
=>△MCI = △DCI (c.g.c)
=> góc CMI = góc CDI (2 góc tương ứng)
Vì góc ADC - góc CDI = góc BDA
Góc CMB - góc CMI = góc BMI
mà góc ADC = góc CMB = 180o
góc CDI = góc CMI (cmt)
=>góc BDA = góc BMI
Ta lại có góc ABD = góc IBM (BD là tia phân giác)
=> góc BDA + góc ABD = góc BMI + góc IBM
Xét △ABD vuông tại A có:
góc BDA + góc ABD = 90o(t/c)
=>góc BMI + góc IBM = 90o
Xét △BIM có
góc BIM + góc BMI + góc IBM = 180o (đ/n)
hay góc BIM + 90o = 180o
=> góc BIM = 180o - 90o = 90o
=> góc BIM = 90o
Áp dụng Pitago có BC=\(\sqrt{AB^2+AC^2}=10\)
\(\frac{AD}{CD}=\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}\Rightarrow AD=\frac{3}{5}.CD\)
AD+CD=3/5CD+CD=8/5CD=AC=8\(\Rightarrow CD=5\) vậy AD=3
b/Xét tgiac AHB và CHA có....\(\)\(\Rightarrow\frac{AH}{HC}=\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AH^2}{HC^2}=\frac{9}{16}\)
lại có Ah^2+HC^2=Ac^2=64..Giải tìm Ah và CH k bk nx thì hỏi