Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10cm
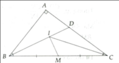
Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{DA}{6}=\dfrac{DC}{10}\)
Ta có: D nằm giữa A và C(gt)
nên DA+DC=AC
hay DA+DC=8(cm)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DA}{6}=\dfrac{DC}{10}=\dfrac{DA+DC}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{DA}{6}=\dfrac{1}{2}\\\dfrac{DC}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DA=6\cdot\dfrac{1}{2}=3\left(cm\right)\\DC=10\cdot\dfrac{1}{2}=5\left(cm\right)\end{matrix}\right.\)
Vậy: DA=3cm; DC=5cm

a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)

câu a bài 2 nhá
a) Gọi D là trung điểm BI => góc IDM = 45 độ
DM // IC ( đường trung bình )
=> góc BIC = 135 độ
=> 180 -1/2( góc B + góc C ) =135 độ
=> góc B + góc C = 90 độ
=> góc A = 90 độ

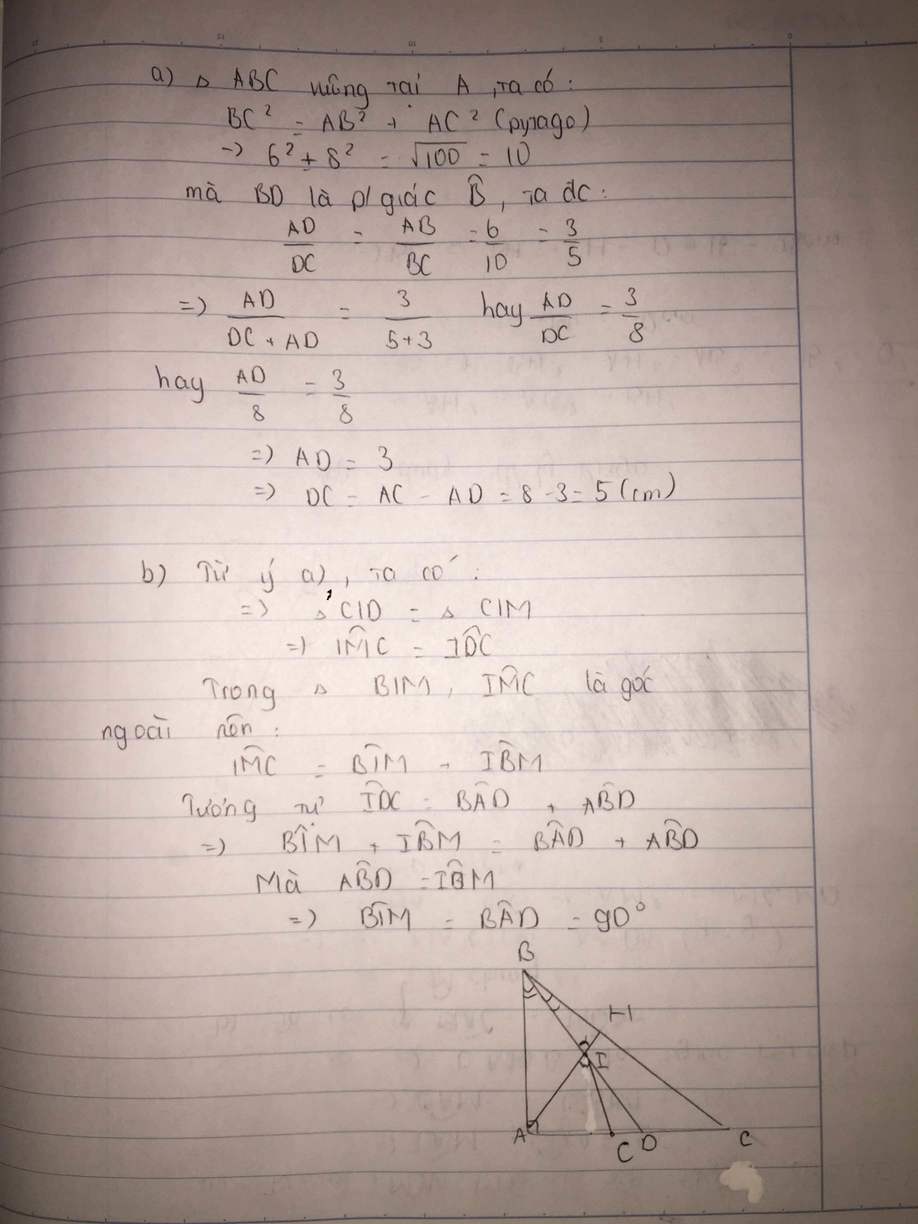
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)
=>\(\dfrac{DA}{6}=\dfrac{DC}{10}\)
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà DA+DC=AC=8cm(D nằm giữa A và C)
nên \(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{8}{8}=1\)
=>\(DA=3\cdot1=3cm;DC=5\cdot1=5cm\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}=5\left(cm\right)\)
mà DC=5cm
nên CM=CD
Xét ΔCDI và ΔCMI có
CD=CM
\(\widehat{DCI}=\widehat{MCI}\)
CI chung
Do đó: ΔCDI=ΔCMI
=>\(\widehat{CID}=\widehat{CIM}\) và \(\widehat{IMC}=\widehat{IDC}\)(3)
Ta có: \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}\)(góc IDC là góc ngoài tại đỉnh D của ΔABD)
nên \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}=90^0+\widehat{ABD}\)(2)
Xét ΔBIM có \(\widehat{IMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{IMC}=\widehat{MIB}+\widehat{MBI}\left(1\right)\)
Từ (1),(2),(3) suy ra \(\widehat{MIB}+\widehat{MBI}=90^0+\widehat{ABD}\)
mà \(\widehat{MBI}=\widehat{ABD}\)
nên \(\widehat{MIB}=90^0\)