Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔAMC có ME là phân giác
nên AE/EC=AM/MC
=>AD/DB=AE/EC
=>ED//BC
b: Xét ΔABM có DI//BM
nên DI/BM=AI/AM
Xét ΔACM có EI//MC
nên EI/CM=AI/AM
=>DI/BM=EI/CM
=>DI=EI

a) 
b) ta có MD là tia phân giác của \(\widehat{AMB}\), ME là tia phân giác của \(\widehat{AMC}\)
=> \(\widehat{AMD}=\widehat{DMB}=\dfrac{1}{2}\widehat{AMB}\) và \(\widehat{AME}=\widehat{EMC}=\dfrac{1}{2}\widehat{AMC}\)
=> \(\widehat{AME}+\widehat{AMD}=\dfrac{\widehat{AMC}+\widehat{AMB}}{2}=\dfrac{180^o}{2}=90^o\)
Ta có \(\widehat{EMC}=\widehat{MED}\)(do ED//BC)
mà \(\widehat{EMC}=\widehat{EMI}\)
=> \(\widehat{EMI}=\widehat{MEI}\)=> tam giác EIM cân tại I
=> EI=IM
cmtt : IM=ID
=> EI=IM=MD
=> IM = \(\dfrac{1}{2}\left(EI+ID\right)=\dfrac{1}{2}ED\)(ĐPCM)

Hình bạn tự vẽ nha.
a, \(\Delta ABC\) có: AM là đường trung tuyến của \(\Delta ABC\)\(\Rightarrow BM=MC\), \(AI=\frac{2}{3}AM\)
\(\Delta AMB\)có: MD là phân giác của \(\widehat{AMB}\)\(\Rightarrow\frac{AD}{DB}=\frac{AM}{MB}\)(tính chất đường phân giác trong tam giác) (1)
\(\Delta AMC\)có: ME là phân giác của \(\widehat{AMC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)(tính chất đường phân giác trong tam giác) (2)
Từ (1), (2) và \(BM=MC\left(cmt\right)\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}\)
\(\Delta ABC\)có: \(\frac{AD}{DB}=\frac{AE}{EC}\left(cmt\right)\Rightarrow DE//BC\)(định lý Ta-lét đảo)
b, \(\Delta ABM\)có: \(DI//BM\left(cmt\right)\Rightarrow\frac{DI}{BM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (3)
\(\Delta AMC\)có: \(IE//MC\left(cmt\right)\Rightarrow\frac{IE}{CM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (4)
Từ (3), (4) và \(BM=MC\left(cmt\right)\Rightarrow DI=IE\)
c, Ta có: \(\frac{IE}{CM}=\frac{AI}{AM}\left(cmt\right)\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}AM}{AM}\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}.10}{10}\)\(\Leftrightarrow\frac{IE}{15}=\frac{2}{3}\)\(\Leftrightarrow IE=10\left(cm\right)\)

1: Xet ΔMAB co MD là phân giác
nen AD/DB=AM/MB=AM/MC
Xét ΔMCA có ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>DE//BC
2: Xét ΔABM có DG//BM
nên DG/BM=AG/AM
Xét ΔACM có EG//MC
nên EG/MC=AG/AM
=>DG/BM=EG/MC
mà BM=MC
nên DG=EG
=>G là trung điểm của DE
Để G là trung điểm của AM thì ADME là hình bình hành
=>DM//AC
=>D là trung điểm của AB
=>E là trung điểm của BC
=>AM/MB=AD/DB=1
=>AM=1/2BC
=>góc BAC=90 độ

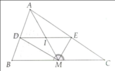
a) Do AM là đường trung tuyến của ∆ABC (gt)
⇒ M là trung điểm của BC
⇒ MB = MC
∆AMB có:
MD là tia phân giác của ∠AMB (gt)
⇒ AD/BD = AM/BM
∆AMC có:
ME là tia phân giác của ∠AMC (gt)
⇒ AE/CE = AM/MC
Mà MB = MC (cmt)
⇒ AD/BD = AE/CE
∆ABC có:
AD/BD = AE/CE (cmt)
⇒ DE // BC (định lý Thales đảo)
b) Do DE // BC (cmt)
⇒ DO // BM và OE // MC
∆ABC có:
DE // BC (cmt)
⇒ AD/AB = AE/AC
∆ABM có:
DO // BM (cmt)
⇒ AD/AB = OD/BM
∆ACM có:
OE // MC (cmt)
⇒ AE/AC = OE/MC
Mà AD/AB = AE/AC (cmt)
⇒ OD/BM = OE/MC
Mà MB = MC (cmt)
⇒ OD = OE
⇒ O là trung điểm của DE
c) Do PQ // BC (gt)
DE // BC (cmt)
⇒ DE // PQ
∆MPQ có:
DE // PQ (cmt)
⇒ DE/PQ = ME/MQ (1)
Do DE // PQ (cmt)
⇒ OE // AQ
∆MAQ có:
OE // AQ (cmt)
⇒ ME/MQ = MO/MA (2)
Từ (1) và (2) ⇒ DE/PQ = MO/MA