Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = cos α cos β − sin β sin α = cos α sin α − cos α sin α = 0 .
Chọn A.
Hai góc α và β bù nhau nên sin α = sin β ; cos α = − cos β .
Do đó P = cos α cos β − sin β sin α = − cos 2 α − sin 2 α = − sin 2 α + cos 2 α = − 1 .
Chọn C.
Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = sin α cos β + sin β cos α = sin 2 α + cos 2 α = 1 .
Chọn B.
Đáp án: B
Số tập hợp con chứa α, β của A là: {α, β }; {α, β, γ };{α, β, ε};{α, β, μ };{α, β, γ, ε };{α, β, γ, μ };{α, β, ε, μ };{α, β, γ, ε, μ }
Chọn A.
Hai góc α và β phụ nhau nên sinα = cosβ và cosα = sinβ.
Do đó, A = cosα.cosβ - sinα.sinβ = cosαsinα - cosα.sinα = 0.
1. Phương trình d có dạng:
\(y=2\left(x-1\right)+1\Leftrightarrow y=2x-1\)
2. Do d tạo chiều dương trục Ox một góc 30 độ nên d có hệ số góc \(k=tan30^0=\dfrac{\sqrt{3}}{3}\)
Phương trình d:
\(y=\dfrac{\sqrt{3}}{3}\left(x-1\right)+2\Leftrightarrow y=\dfrac{\sqrt{3}}{3}x+\dfrac{6-\sqrt{3}}{3}\)
3. Do d tạo với trục Ox một góc 45 độ nên có hệ số góc thỏa mãn:
\(\left|k\right|=tan45^0\Rightarrow\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=1\left(x-3\right)+4\\y=-1\left(x-3\right)+4\end{matrix}\right.\)
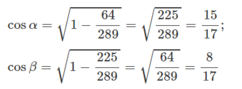
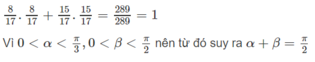
Vậy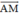
là vec tơ cùng hướng với 
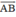và có độ dài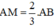 
Vậy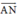
là vec tơ ngược hướng với 
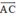và có độ dài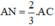 
(Do hai vec tơ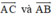
không cùng phương nên chỉ bằng nhau khi chúng đồng thời bằng 0→).
Vậy MN song song với BC khi và chỉ khi α = β.