Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔAED vuông tại E
=>AD là cạnh lớn nhất trong ΔAED
=>AD>AE
Ta có: ΔCFD vuông tại F
=>CD là cạnh lớn nhất trong ΔCFD
=>CD>CF
Ta có: AD>AE
CD>CF
Do đó: AD+CD>AE+CF
=>AC>AE+FC

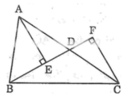
+ AE là đường vuông góc hạ từ đỉnh A xuống đường thẳng BF
⇒ AE < AD. ( quan hệ đường vuông góc và đường xiên). (1)
+ CF là đường vuông góc hạ từ đỉnh C xuống đường thẳng BF
⇒ CF < CD ( quan hệ đường vuông góc và đường xiên). (2)
Từ (1) và (2) vế cộng vế ta được: AE + CF < AD + CD = AC.

a) Trong \(\Delta BHE,\widehat{BHE}=90^o\) có:
\(\Rightarrow BE>BH\left(ch>chv\right)\left(1\right)\)
b) Trong \(\Delta CEK,\widehat{CEK}=90^o\) có:
\(\Rightarrow CE>CK\left(ch>chv\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow BE+CE>BH+CK\)
\(\Rightarrow BC>BH+CK\)

5. Sửa đề: c/m \(AC>AE+CF\). Điểm D nằm giữa A và C.
-Ta có: A∉BD và AE⊥BD tại E (gt).
\(\Rightarrow\)AE là đường vuông góc còn AD là đường xiên.
\(\Rightarrow AE< AD\) (quan hệ giữa đường vuông góc và đường xiên) (1)
-Ta có: C∉BD và CF⊥BD tại F (gt).
\(\Rightarrow\)CF là đường vuông góc còn CD là đường xiên.
\(\Rightarrow CF< CD\) (quan hệ giữa đường vuông góc và đường xiên) (2)
-Từ (1) và (2) suy ra: \(AE+CF< AD+CD=AC\).
6.

a: ΔBHA vuông tại H
=>BH<AB
ΔCKA vuông tại K
=>CK<AC
=>BH+CK<AB+AC
b: ΔBDH vuông tại H
=>BH<BD
ΔCKD vuông tại K
=>CK<CD
=>BH+CK<BD+CD=BC

Trả lời:
a, BH = AK:
Ta có: ΔABC vuông cân tại A.
=> A1ˆ=A2ˆ=90oA1^=A2^=90o (1)
Cũng có: BH ⊥ AE.
=> ΔBAH vuông tại H.
=> B1ˆ+A2ˆ=90oB1^+A2^=90o (2)
Từ (1) và (2) => A1ˆ=B1ˆA1^=B1^.
Xét ΔBAH và ΔACK có:
+ AB = AC (ΔABC cân)
+ H1ˆ=K1ˆ=90oH1^=K1^=90o (CK ⊥ AE, BH ⊥ AE)
+ A1ˆ=B1ˆ=(cmt)A1^=B1^=(cmt)
=> ΔBAH = ΔACK (cạnh huyền - góc nhọn)
=> BH = AK (2 cạnh tương ứng)
b, ΔMHK vuông cân:
Xét ΔAMH và ΔCMK có:
+ AH = CK (ΔABH = ΔCAK)
+ MH = MK (ΔMBH = ΔMAK)
+ AM = CM (AM là trung tuyến)
=> ΔAMH = ΔCMK (c - c - c)
=> AMHˆ=CMKˆAMH^=CMK^ (2 góc tương ứng)
mà AMHˆ+HMCˆ=90oAMH^+HMC^=90o
=> CMKˆ+HMCˆ=90oCMK^+HMC^=90o
hay HMKˆ=90oHMK^=90o.
ΔHMK có MK = MH và MHKˆ=90oMHK^=90o.
=> ΔHMK vuông cân tại M.
~Học tốt!~

A) XÉT \(\Delta BDE\)VUÔNG TẠI E
CÓ BD LÀ CẠNH HUYỀN, BE LÀ CẠNH GÓC VUÔNG
( ĐỊNH LÍ: TRONG 1 TAM GIÁC VUÔNG THÌ CẠNH HUYỀN LUÔN LỚN HƠN 2 CẠNH GÓC VUÔNG)
=> BD>BE( ĐỊNH LÍ)
B) XÉT \(\Delta CDF\)VUÔNG TẠI F
CÓ CD LÀ CẠNH HUYỀN; CF LÀ CẠNH GÓC VUÔNG
=> CD> CF
MÀ BD>BE ( PHẦN A)
=> CD+BD > BE+ CF
=> BC > BE + CF
MK KO KẺ HÌNH ĐÂU
MK KO BIẾT NÓ ĐÚNG HAY SAI, MK CHỈ ĐC NHƯ VẬY THÔI!
BN KẺ HÌNH LÊN GIÚP MK NHA XEM CÓ GIỐNG HÌNH CỦA MK KO, HAY MK KẺ SAI!
CHÚC BN HỌC TỐT!!!
