Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ sau:
a) Vì AB = AC => ΔABC cân
=> \(\widehat{B_2}=\widehat{C_1}\)
Xét ΔABM và ΔACM có:
AB = AC (gt)
\(\widehat{B_2}=\widehat{C_1}\left(cmt\right)\)
BM = CM (gt)
=> ΔABM = ΔACM(c.g.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^o\) (kề bù)
=> \(\widehat{AMB}=\widehat{AMC}=\frac{180^o}{2}=90^o\)
=> AM \(\perp\) BC(đpcm)
b) Ta có: \(\widehat{B_2}=\widehat{C_1}\) và \(\widehat{B_1}+\widehat{B_2}=180^o;\widehat{C_1}+\widehat{C_2}=180^o\)
=> \(\widehat{B_1}=\widehat{C_2}\)
Xét ΔABD và ΔACE có:
AB = AC(gt)
\(\widehat{B_1}=\widehat{C_2}\left(cmt\right)\)
BD = CE (gt)
=> ΔABD = ΔACE(c.g.c)
=> \(\widehat{BAD}=\widehat{CAE}\) (2 góc tương ứng)
mà \(\widehat{BAM}=\widehat{CAM}\) (ΔABM = ΔACM)
=> \(\widehat{BAD}+\widehat{BAM}=\widehat{CAE}+\widehat{CAM}\)
=> AM là tia p/g của \(\widehat{DAE}\) (đpcm)

Xét tứ giác EDCB có
A là trung điểm chung của EC và DB
nên EDCB là hình bình hành
=>ED//BC và ED=BC
Xét tứ giác ENCM có
EN//CM
EN=CM
Do đo: ENCM là hìnhbình hành
=>EC căt NM tại trug điểm của mỗi đường
=>M,A,N thẳng hàng
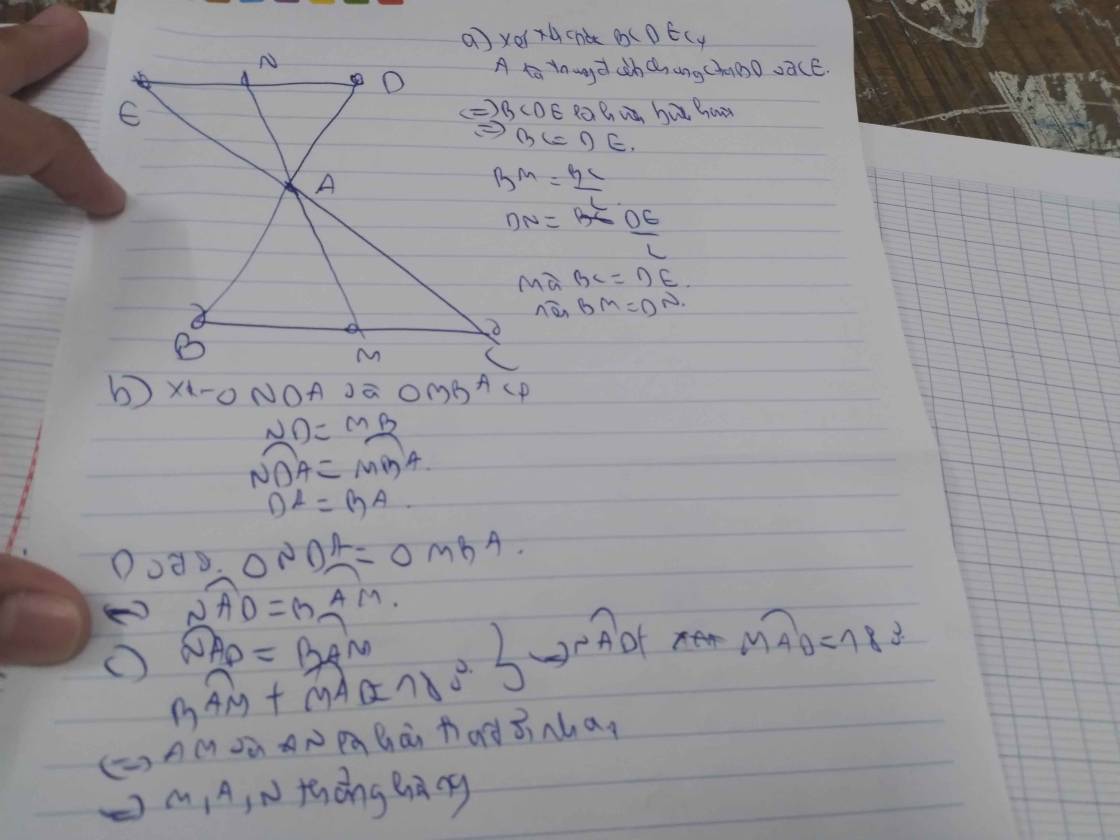
1: Xét tứ giác BEDC có
A là trung điểm chung của BD và EC
nên BEDC là hình bình hành
=>BC=DE
=>BM=DN
2: Xét ΔABM và ΔADN có
AB=AD
góc ABM=góc ADN
BM=DN
Do đo: ΔABM=ΔADN
=>góc BAM=góc DAN
3: góc BAM=góc DAN
mà góc BAM+góc MAD=180 độ
nên góc DAN+góc MAD=180 độ
=>M,A,N thẳng hàng