Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

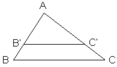
Áp dụng hệ quả trên ta có: Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
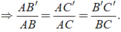
Khi đó ta có: AB'/AB = AC'/AC ⇔ 2/8 = 3/AC ⇒ AC = (3.8)/2 = 12( cm )

Lời giải :
Ta có : \(\frac{AB'}{AB}=\frac{AC'}{AC}\)( GT ) ( 1 )
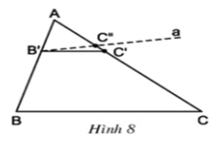
+) Đường thẳng a đi qua B' song song với BC ( GT )
\(B'C''//BC\)( vì đường thẳng a cắt AC tại C'' )
\(\Rightarrow\frac{AB'}{AB}=\frac{AC''}{AC}\)( Định lí Ta lét ) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow AC'=AC''\)

Ta có: \(\dfrac{AB}{AM}=\dfrac{4}{2}=2\)
\(\dfrac{AC}{AN}=\dfrac{6}{3}=2\)
Do đó: \(\dfrac{AB}{AM}=\dfrac{AC}{AN}\)(=2)
Xét ΔABC và ΔAMN có
\(\dfrac{AB}{AM}=\dfrac{AC}{AN}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔABC\(\sim\)ΔAMN(c-g-c)


Ta có:
\(\dfrac{AB}{AM}=\dfrac{4}{2}=2\)
\(\dfrac{AC}{AN}=\dfrac{6}{3}=2\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AC}{AN}=2\)
Xét \(\Delta ABC\) và \(\Delta AMN\) có:
\(\dfrac{AB}{AM}=\dfrac{AC}{AN}=2\)
\(\widehat{A}\) chung
\(\Rightarrow\Delta ABC\) đồng dạng \(\Delta AMN\) (c-g-c)

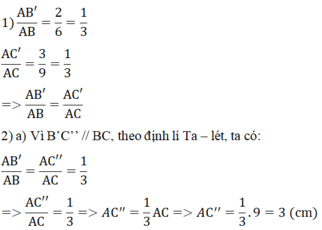
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

Theo định lý Ta - let ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
\(\Leftrightarrow\dfrac{4}{6}=\dfrac{3}{AC}\)
\(\Rightarrow\dfrac{2}{3}=\dfrac{1}{AC}\)
\(\Rightarrow2AC=3\)
\(\Rightarrow AC=\dfrac{2}{3}\)
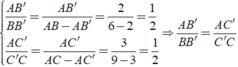
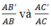
Hình bn tự vẽ nhé.
Ta có
• \(\frac{AB'}{AB}=\frac{2}{6}=\frac{1}{3}\left(1\right)\)
•\(\frac{AC'}{AC}=\frac{3}{9}=\frac{1}{3}\left(2\right)\)
Từ (1) và (2) => \(\frac{AB'}{AB}=\frac{AC'}{AC}\)
Xét tam giác ABC có B' thuộc AB, C' thuộc AC và \(\frac{AB'}{AB}=\frac{AC'}{AC}\)
=> B'C' // BC ( theo định lí Ta-lét đảo)