Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có A, E, F, K, H cùng thuộc đường tròn đường kính AH.
b) Ta có \(\widehat{AMN}=90^o-\widehat{OAB}=90^o-\dfrac{180^o-\widehat{AOB}}{2}=\dfrac{\widehat{AOB}}{2}=\widehat{ACB}\).
Suy ra tứ giác BMNC nội tiếp và \(\Delta SMB\sim\Delta SCN\left(g.g\right)\) nên \(SM.SN=SB.SC\).
c) Ta có \(\widehat{QCB}=\widehat{QAB}=\widehat{HCB};\widehat{QBC}=\widehat{HBC}\) nên Q, H đối xứng với nhau qua BC.
Mà S thuộc BC nên SH = SQ.
Ta lại có \(\widehat{SHB}=\widehat{BHF}-\widehat{MHF}=\widehat{BAC}-\left(90^o-\widehat{AMH}\right)=\widehat{BAC}+\widehat{ACB}-90^o=90^o-\widehat{ABC}=\widehat{SCH}\Rightarrow\Delta SHB\sim\Delta SCH\left(g.g\right)\Rightarrow SQ^2=SH^2=SB.SC\).
d) I là điểm nào vậy bạn?

a) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
nên BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(AE\cdot AC=AB\cdot AF\)

a: góc AMH+góc ANH=180 độ
=>AMHN nội tiếp
b: Vì góc BMC=góc BNC=90 độ
nên BMNC nội tiếp
=>góc HMN=góc HBC
mà goc MHN=góc BHC
nên ΔHMN đồng dạng vơi ΔHBC
=>HM/HB=MN/BC
=>HM*BC=HB*MN
c: góc NMH=góc HAC
góc KMH=góc NBC
mà góc HAC=góc NBC
nên góc NMH=góc KMH
=>MH là phân giác của góc NMK(1)
góc MKH=góc ABN
góc NKH=góc ACM
góc ABN=góc ACM
Do đó: góc MKH=góc NKH
=>KH là phân giác của góc MKN(2)
Từ (1), (2) suy ra H là tâm đường tròn nội tiếp ΔKMN
Lời giải:
*** Mình chưa thấy điểm $I$ có vai trò gì trong bài này.
Gọi $D$ là giao điểm $BC, AN$ và $L$ là giao $AN$ với $(O)$
Dễ thấy $\triangle ABN=\triangle MCN$ do:
$AB=MC$ (tính chất cung bị chặn bởi 2 dây song song)
$NB=NC$
$\widehat{ABN}=\frac{1}{2}\text{sđc(AB>)}=\frac{1}{2}\text{sđc(MC>)}=\widehat{MCN}$
Do đó:
$\widehat{BAD}=\widehat{BAN}=\widehat{CMN}=\widehat{CAH}$
$\Rightarrow \widehat{BAH}=\widehat{CAD}$
Ta có:
$\frac{HB}{CH}=\frac{S_{ABH}}{S_{ACH}}=\frac{AB.AH.\sin BAH}{AC.AH.\sin CAH}=\frac{AB.\sin BAH}{AC\sin CAH}$
$=\frac{AB}{AC}.\frac{\sin BAH}{\sin CAH}=\frac{AB}{AC}.\frac{\sin CAD}{\sin BAD}=\frac{AB}{AC}.\frac{\sin CAL}{\sin BAL}=\frac{AB}{AC}.\frac{\sin CBL}{\sin BCL}=\frac{AB}{AC}.\frac{LC}{BL}(*)$
Mà:
Dễ cm $\triangle ABN\sim \triangle BLN, \triangle ACN\sim \triangle CLN$
$\Rightarrow \frac{AB}{BL}=\frac{BN}{LN}=\frac{CN}{LN}=\frac{AC}{CL}$
$\Rightarrow \frac{LC}{BL}=\frac{AC}{AB}(**)$
Từ $(*); (**)\Rightarrow \frac{BH}{HC}=\frac{AB}{AC}.\frac{AC}{AB}=1$
$\Rightarrow BH=HC$ nên $H$ là trung điểm của $BC$
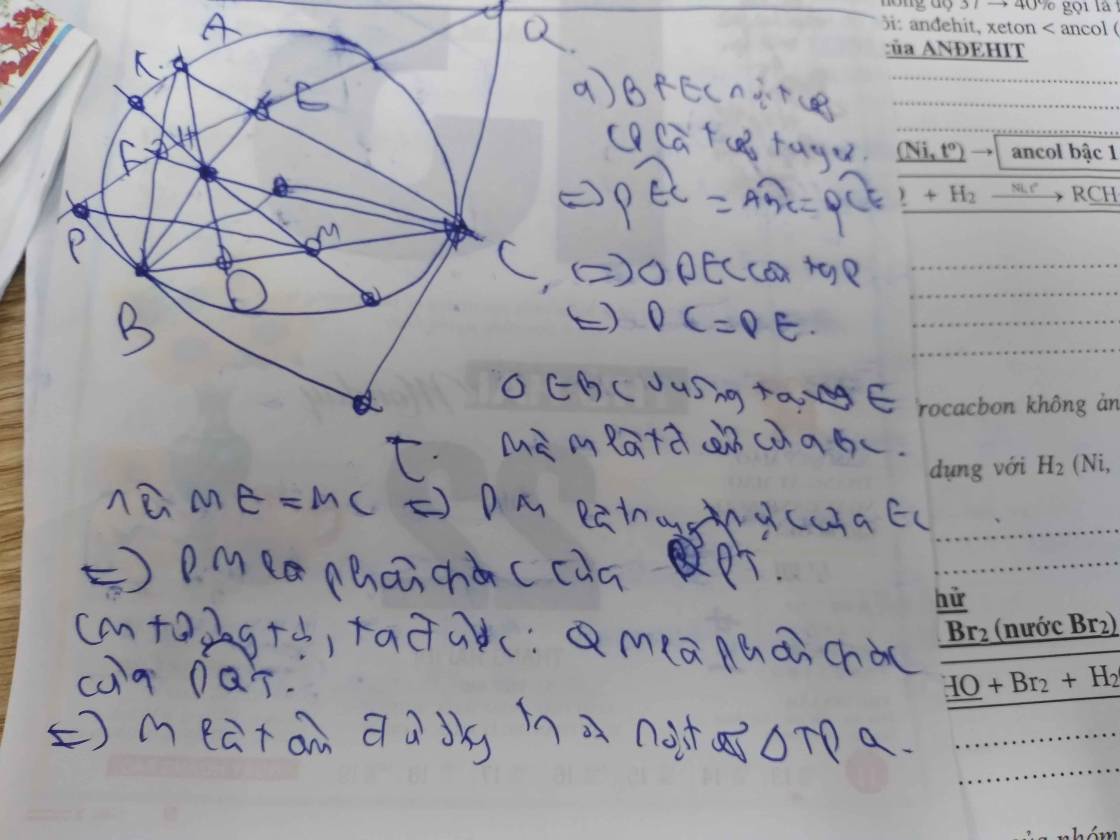
Hình vẽ: