Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

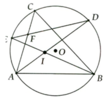
a, B I D ^ = 1 2 s đ D E ⏜ = D B E ^ => ∆BID cân ở D
b, Chứng minh tương tự: DIEC cân tại E, DDIC cân tại D
=> EI = EC và DI = DC
=> DE là trung trực của CI
c, F Î DE nên FI = FC
=> F I C ^ = F C I ^ = I C B ^ => IF//BC

a/ Ta có : \(B\widehat{I}D=\frac{1}{2}\left(\widebat{AE}+\widebat{BD}\right)\)
Mà \(\widebat{BD}=\widebat{DC}\); \(\widebat{AE}=\widebat{EC}\)( tự CM nha )
Nên \(B\widehat{I}D=\frac{1}{2}\left(\widebat{EC}+\widebat{DC}\right)=\frac{1}{2}\widebat{ED}\)
Mặc khác \(I\widehat{B}D=\frac{1}{2}\widebat{ED}\)
=> \(B\widehat{I}D=I\widehat{B}D\)
=> tam giác BDI cân tại D
b/ C/m tương tự => tam giác IDC cân tại D
Gọi K là giao điểm IC và DF
Ta có : \(I\widehat{D}K=C\widehat{D}K\)( 2 góc n.t chắn 2 cung = nhau )
=> DK là đường phân giác tam giác IDC
Mà tam giác IDC cân tại D
Nên DK cũng là đường cao , đường trung tuyến tam giác IDC
=> K là trung điểm IC và ED vuông góc IC tại K
=> DE là đường trung trực IC
c/ Ta có DE là đường trung trực IC
Mà \(F\in DE\)
Nên \(FI=FC\)
=> tam giác FIC cân tại F => \(F\widehat{I}C=F\widehat{C}I\)
Mà \(F\widehat{C}I=B\widehat{C}I\)( CI là tia phân giác \(A\widehat{C}B\))
Nên \(F\widehat{IC}=I\widehat{C}B\)
Mặc khác 2 góc này ở vị trí so le trong => \(IF//BC\)

Lời giải:
a) Ta có:
\(\widehat{IBD}=\widehat{EBD}=\frac{1}{2}(\text{sđc(EC)}+\text{sđc(CD)})\)
\(\widehat{BID}=\frac{1}{2}(\text{sđc(BD)}+\text{sđc(AE)})\)
Mà $\text{sđc(EC)}=\text{sđc(AE)}$ và $\text{sđc(CD)}=\text{sđc(BD)}$ do $AD, BE$ là tia phân giác $\widehat{A}, \widehat{B}$
$\Rightarrow \widehat{IBD}=\widehat{BID}$ nên $BID$ là tam giác cân ở $D$
b) Tam giác $BID$ cân tại $D$ nên $BD=ID$$D$ nằm chính giữa cung $BC$ nên $BD=CD$
$\Rightarrow DI=DC(1)$
Lại có: $\widehat{BID}=\widehat{IBD}$
$\widehat{BID}=\widehat{AIE}$
$\widehat{IBD}=\widehat{IAE}$ (góc nt cùng nhìn cung $EC$)
$\Rightarrow \widehat{AIE}=\widehat{IAE}$ nên tam giác $IAE$ cân tại $E$
$\Rightarrow EI=EA=EC(2)$
Từ $(1);(2)$ suy ra $DE$ là trung trực của $IC$
c) $F\in DE$ là đường trung trực $IC$ nên $FI=FC$
$\Rightarrow \triangle FIC$ cân tại $F$
$\Rightarrow \widehat{FIC}=\widehat{FCI}$
Mà $\widehat{FCI}=\widehat{ICB}$ nên $\widehat{FIC}=\widehat{ICB}$
Hai góc này ở vị trí so le trong nên $IF\parallel BC$ (đpcm)

