K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
13 tháng 8 2019
a, B I D ^ = 1 2 s đ D E ⏜ = D B E ^ => ∆BID cân ở D
b, Chứng minh tương tự: DIEC cân tại E, DDIC cân tại D
=> EI = EC và DI = DC
=> DE là trung trực của CI
c, F Î DE nên FI = FC
=> F I C ^ = F C I ^ = I C B ^ => IF//BC

Lời giải:
a) Ta có:
\(\widehat{IBD}=\widehat{EBD}=\frac{1}{2}(\text{sđc(EC)}+\text{sđc(CD)})\)
\(\widehat{BID}=\frac{1}{2}(\text{sđc(BD)}+\text{sđc(AE)})\)
Mà $\text{sđc(EC)}=\text{sđc(AE)}$ và $\text{sđc(CD)}=\text{sđc(BD)}$ do $AD, BE$ là tia phân giác $\widehat{A}, \widehat{B}$
$\Rightarrow \widehat{IBD}=\widehat{BID}$ nên $BID$ là tam giác cân ở $D$
b) Tam giác $BID$ cân tại $D$ nên $BD=ID$$D$ nằm chính giữa cung $BC$ nên $BD=CD$
$\Rightarrow DI=DC(1)$
Lại có: $\widehat{BID}=\widehat{IBD}$
$\widehat{BID}=\widehat{AIE}$
$\widehat{IBD}=\widehat{IAE}$ (góc nt cùng nhìn cung $EC$)
$\Rightarrow \widehat{AIE}=\widehat{IAE}$ nên tam giác $IAE$ cân tại $E$
$\Rightarrow EI=EA=EC(2)$
Từ $(1);(2)$ suy ra $DE$ là trung trực của $IC$
c) $F\in DE$ là đường trung trực $IC$ nên $FI=FC$
$\Rightarrow \triangle FIC$ cân tại $F$
$\Rightarrow \widehat{FIC}=\widehat{FCI}$
Mà $\widehat{FCI}=\widehat{ICB}$ nên $\widehat{FIC}=\widehat{ICB}$
Hai góc này ở vị trí so le trong nên $IF\parallel BC$ (đpcm)
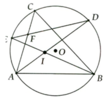
Hình vẽ: