Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: CD//AB

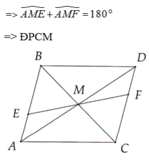
a: Xét tứ giác AEDB có
M là trung điểm chung của AD và EB
=>AEDB là hình bình hành
=>AE=DB và AE//DB
=>AE//BC
b: BD=AE
mà AE<AC
nên BD<AC
c: Xét tứ giác AFDC có
M là trung điểm chung của AD và FC
=>AFDC là hình bình hành
=>AF//DC
mà AE//DC
nên A,E,F thẳng hàng
Cho mik hỏi chút với ạ, làm sao bạn chứng minh được AE<AC ạ?

a/ Xét △ABM và △DMC có:
\(\begin{matrix}AM=MD\left(gt\right)\\MB=MC\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\) (đpcm).
b/ Ta có: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\hat{MAB}=\hat{MDC}\); hai góc ở vị trí so le trong.
Vậy: AB // CD (đpcm).
c/ Xét △BAE có:
\(\begin{matrix}BH\perp AE\left(gt\right)\\AH=HE\left(gt\right)\end{matrix}\)
⇒ BH vừa là đường cao, vừa là đường trung tuyến.
⇒ △BAE cân tại B.
\(\Rightarrow BE=BA\). Mà \(AB=CD\left(\Delta AMB=\Delta DMC\right)\)
Vậy: BE = CD (đpcm).

Câu hỏi của Tuấn Anh Nguyễn - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo link bài làm tương tự nhé!

b1 :
tự cm tam giác ABC vuông
=> góc ABC + góc ACB = 90 (đl)
BI là pg của góc ABC => góc IBC = góc ABC : 2
CI là pg của góc ACB => góc ICB = góc ACB : 2
=> góc IBC + góc ICB = (góc ABC + góc ACB) : 2
=> góc IBC + góc ICB = 45
xét tam giác IBC => góc IBC + góc ICB + góc BIC = 180
=> góc BIC = 135

a: Xét ΔAMD và ΔCMB có
MA=MC
góc AMD=góc CMB
MD=MB
=>ΔAMD=ΔCMB
b: Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
=>ΔABC=ΔCDA
c: Sửa đề: MF vuông góc BC
Xét ΔMBF và ΔMDE có
MB=MD
góc MBF=góc MDE
BF=DE
=>ΔMBF=ΔMDE
=>góc MFB=90 độ
=>MF vuông góc BC
d: ΔMFB=ΔMED
=>góc FMB=góc EMD
=>góc EMD+góc DMF=180 độ
=>M,E,F thẳng hàng