Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Giả sử m không cắt AB, AC. Thật vậy ta suy ra m // AB và m // AC. Suy ra AB // AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.
b) Giả sử m không cắt AC. Thật vậy ta suy ra m // AC. Suy ra AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.

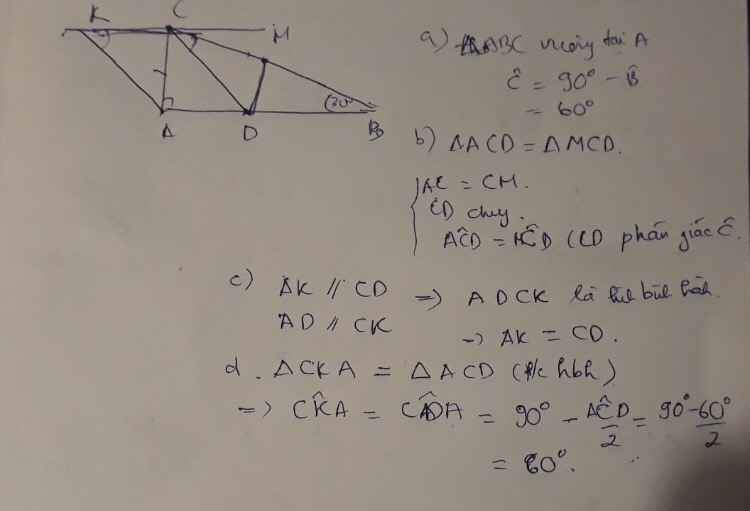
a: Xét ΔBAE và ΔBME có
BA=BM
AE=ME
BE chung
=>ΔBAE=ΔBME
b: Xet ΔBAK và ΔBMK có
BA=BM
góc ABK=góc MBK
BK chung
=>ΔBAK=ΔBMK
=>góc BMK=90 độ
=>MK vuông góc AC
c: Xét tứ giác KFMQ có
MF//KQ
MF=KQ
=>KFMQ là hình bình hành
=>MQ//FK
=>góc CMQ=góc CBK=góc ABK

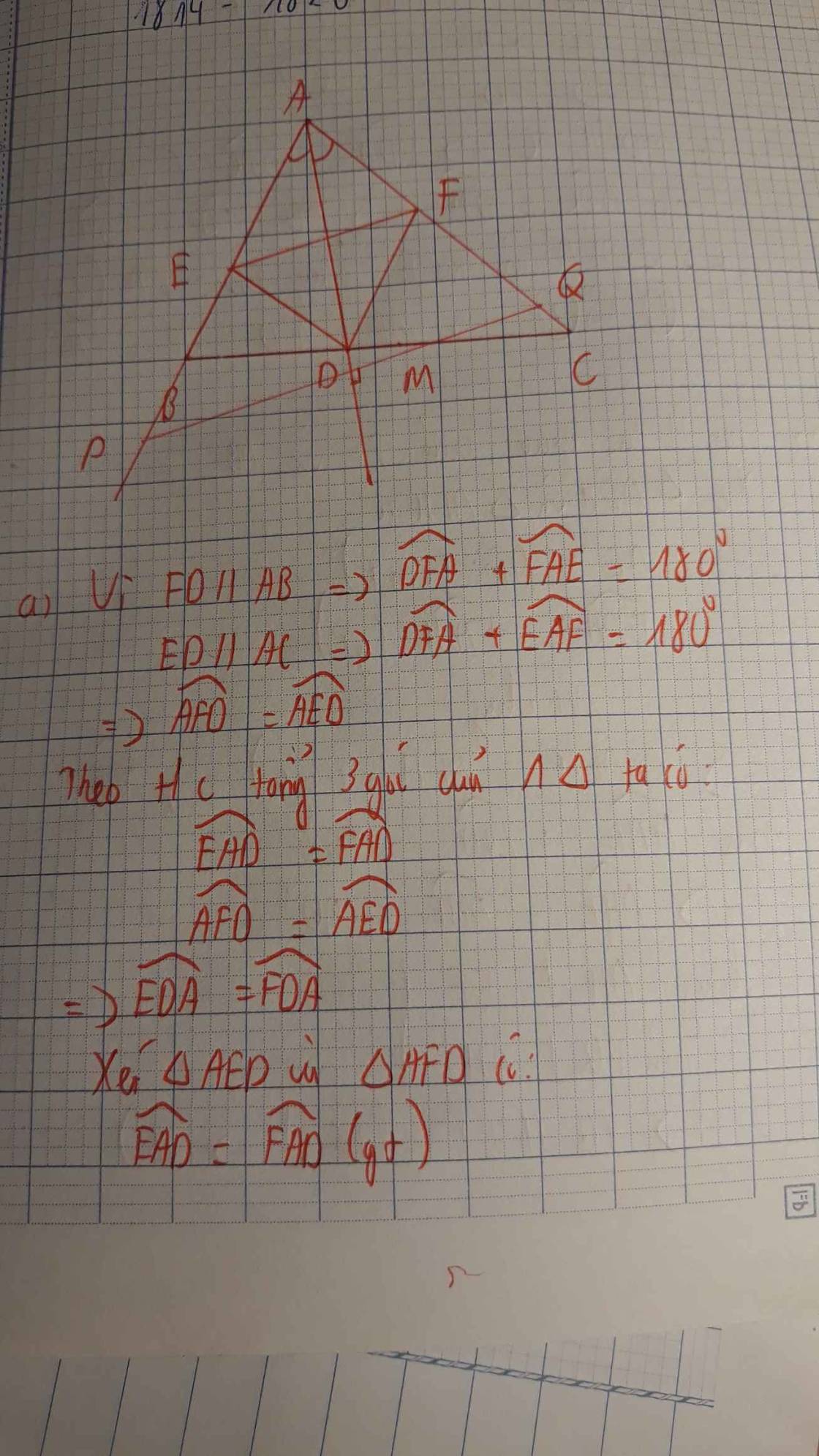
a/ tgiác ACD và tgiác AME là hai tgiác vuông tại A.
AD = AE (gt)
góc(ADC) = góc (AEM) (góc có cạnh tương ứng vuông góc)
=> tgiácACD = tgiácAME (g.c.g)
b/ ta có: AG//EH (cùng vuông góc với CD)
=> AG // IH
mà gt => AI // GH
vậy AGHI là hình bình hành
=>AG = IH.
mặt khác theo cm trên ta có: tgiác ACD = tgiác AME
=> AM = AC = AB
=> A là trung điểm BM, mà AI // BC
=> AI là đường trung bình của tgiác MBH
=> I là trung điểm của MH.
vậy: IM = IH = AG
có: AM = AB
góc BAG = góc AMI (so le trong)
=> tgiác AGB = tgiác MIA ( c.g.c)
c/ có AG//MH, A là trung điểm BM
=> AG là đường trung bình của tgiácBMH
=> G là trung điểm BH
hay BG = GH.


Chọn B