Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)

Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
b)

Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.

a: ΔABM=ΔACM
=>BM=CM
=> M là trung điểm của BC
b: ΔAMC=ΔAMB
=>góc MAC=góc MAB và AC=AB
=>AM là phân giác của góc BAC
AB=AC
MB=MC
=>AM là trung trực của BC
=>AM vuông góc BC

Xét \(\Delta ABC\)có
AM là đường trung tuyến ( M là trung điểm của BC )
AM là đường phân giác ( AM là tia phân giác của \(\widehat{BAC}\))
Nên \(\Delta ABC\)cân tại A ( tam giác có đường trung tuyến đồng thời là đường phân giác )

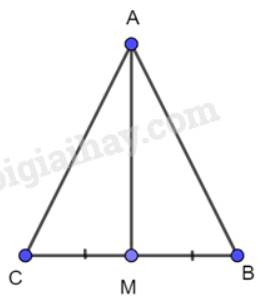
Xét 2 tam giác AMB và AMC có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
\(\Rightarrow\) \(\Delta AMB=\Delta AMC\) (c.c.c)
\(\Rightarrow\) \(\widehat {BAM} = \widehat {CAM}\)(2 góc tương ứng).
Mà tia AM nằm trong góc BAC
\(\Rightarrow\) AM là phân giác của góc BAC
Mặt khác: Do \(\Delta AMB=\Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}\)(2 góc tương ứng) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
Nên: \(\widehat {AMB} = \widehat {AMC} = {90^o}\).
Vậy AM vuông góc với BC.

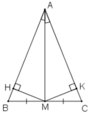
Kẻ MH ⊥ AB, MK ⊥ AC
Xét hai tam giác vuông AHM và AKM, ta có:
∠(AHM) =∠(AKM) = 90o
Cạnh huyền AM chung
∠(HAM) = ∠KAM) (gt)
⇒ ΔAHM = ΔAKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
Xét hai tam giác vuông MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90o
MB = MC ( vì M là trung điểm BC).
MH = MK (chứng minh trên)
⇒ ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.


Tham khảo:
Xét tam giác `ABM` và tam giác `AMC`, ta có :
AM cạnh huyền chung
\(\widehat{AMB}=\widehat{AMC}=90^o\)(góc vuông )
\(\widehat{BAM}=\widehat{MAC}\)(giả thiết)
Do đó tam giác `ABM`=tam giác `AMC`(cạnh huyền-cạnh góc vuông)
\(=>AB=AC\)(hai cạnh tương ứng)
=>tam giác `ABC` cân tại `A.`