Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADCB có
M là trung điểm của đường chéo AC
M là trung điểm của đường chéo BD
Do đó: ADCB là hình bình hành
Suy ra: AD//BC và AD=BC
Xét tứ giác AEBC có
N là trung điểm của đường chéo AB
N là trung điểm của đường chéo CE
Do đó: AEBC là hình bình hành
Suy ra: AE//BC và AE=BC
Ta có: AD//BC
AE//BC
mà AD và AE có điểm chung là A
nên D,A,E thẳng hàng
mà AD=AE(=BC)
nên D và E đối xứng nhau qua A

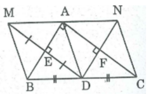
Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng qua điểm A.

a, Vì M là trung điểm AC và BE nên ABCE là hbh
b, Vì ABCE là hbh nên AE//BC;AE=BC(1)
Vì N là trung điểm AB và CF nên ACBF là hbh
Do đó AF//BC;AF=BC(2)
Từ (1)(2) ta được AE trùng AF và AE=AF
Vậy E đx F qua A

a: Xét tứ giác ABCE có
M là trung điểm của AC
M là trung điểm của BE
Do đó: ABCE là hình bình hành

a/ M là trung điểm AC, D đối xứng với B qua M hay M là trung điểm BD
Vậy: ABCD là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành) (đpcm)
===========
b/ N đối xứng với A qua E hay E là trung điểm AN
CE // AD (do CE thuộc BC, ABCD là hình bình hành)
⇒ CE là đường trung bình của △NAB ⇒ C là trung điểm ND
Vậy: D đối xứng với N qua C (đpcm)
a: Xét tứ giác ABCD có
M là trung điểm của đường chéo AC
M là trung điểm của đường chéo BD
Do đó: ABCD là hình bình hành

a: E đối xứng M qua AB
nên AB là trung trực của ME
=>AB vuông góc với ME tại trung điểm của ME
=>AB là phân giác của góc EAM(1)
E đối xứng N qua AC
nên AC là trung trực của NE
=>AC vuông góc với NE tại trung điểm của NE
=>AC là phân giác của góc EAN(2)
Xét tứ giác AIEK có
góc AIE=góc AKE=góc KAI=90 độ
nên AIEK làhình chữ nhật
b: Từ (1), (2) suy ra góc NAM=2*90=180 độ
=>N,A,M thẳng hàng
mà AM=AN
nên A là trung điểm của MN
A B C M N D E
Xét \(\Delta DAM\) và \(\Delta CBM\) có:
\(BM=AM\left(gt\right);\widehat{DMA}=\widehat{CMB}\left(đ.đ\right);DM=MC\left(đ.đ\right)\Rightarrow\Delta DAM=\Delta CBM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DAM}=\widehat{CBM}\) ( 1 )
Tương tự \(\Delta AEN=\Delta CBN\left(c.g.c\right)\Rightarrow\widehat{EAN}=\widehat{BCN}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra:\(\widehat{DAM}+\widehat{EAN}=\widehat{CBM}+\widehat{BCN}\)
\(\Rightarrow\widehat{DAM}+\widehat{EAN}+\widehat{BAC}=\widehat{CBM}+\widehat{BCN}+\widehat{BAC}\Rightarrow\widehat{DAE}=180^0\)
=> D,A,E thẳng hàng.
Mặt khác \(DA=BC;EA=BC\Rightarrow DA+EA=2BC\Rightarrow DE=2BC\Rightarrow DA=EA\Rightarrowđpcm\)