Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sửa đề: BHCK
Xét tứ giác BHCK có
M là trung điểm chung của BC và HK
=>BHCK là hình bình hành
b: BHCK là hình bình hành
=>BH//CK và BK//CH
=>BK vuông góc BA và CK vuông góc CA
c: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>ME=MF
=>ΔMEF cân tại M

a: Xét tứ giác BGCN có
D là trung điểm của đường chéo BC
D là trung điểm của đường chéo GN
Do đó: BGCN là hình bình hành

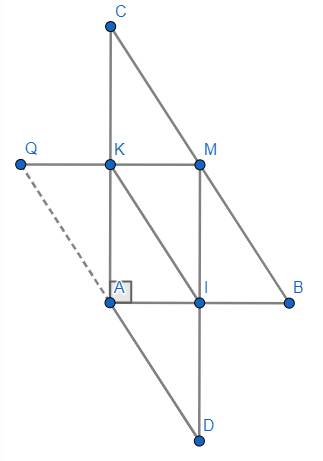
(a) \(I,M\) là trung điểm của \(AB,BC\Rightarrow IM\) là đường trung bình của \(\Delta ABC\Rightarrow\left\{{}\begin{matrix}IM\left|\right|AC\Leftrightarrow MD\left|\right|AC\left(1\right)\\IM=\dfrac{1}{2}AC\end{matrix}\right.\)
Lại có: \(IM=ID\Rightarrow MD=2IM=2\cdot\dfrac{1}{2}AC=AC\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow ADMC\) là hình bình hành (điều phải chứng minh).
(b) \(\left\{{}\begin{matrix}MI\left|\right|AC\left(cmt\right)\\AC\perp AB\left(gt\right)\end{matrix}\right.\Rightarrow MI\perp AB\Rightarrow\hat{AIM}=90^o\left(3\right)\).
\(M,K\) là trung điểm của \(BC,AC\Rightarrow MK\) là đường trung bình của \(\Delta ABC\Rightarrow MK\left|\right|AB\), mà \(AB\perp AC\left(gt\right)\Rightarrow MK\perp AC\Rightarrow\hat{AKM}=90^o\left(4\right)\).
Ta cũng có: \(\hat{A}=90^o\left(5\right)\).
Từ \(\left(3\right),\left(4\right),\left(5\right)\Rightarrow AIMK\) là hình chữ nhật (điều phải chứng minh).
(c) Do \(AIMK\) là hình chữ nhật (chứng minh trên) nên \(\left\{{}\begin{matrix}AK\left|\right|MI\Leftrightarrow AK\left|\right|ID\\AK=MI=ID\end{matrix}\right.\Rightarrow AKID\) là hình bình hành \(\Rightarrow IK\left|\right|AD\left(6\right)\).
Lại có: \(I,K\) là trung điểm của \(MD,MQ\Rightarrow IK\) là đường trung bình của \(\Delta MQD\Rightarrow IK\left|\right|QD\left(7\right)\)
Từ \(\left(6\right),\left(7\right)\Rightarrow Q,A,D\) thẳng hàng (điều phải chứng minh).

a: Xét tứ giác BHCK có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BHCK là hình bình hành

a: Xét tứ giác AFCD có
E là trung điểm chung của AC và FD
=>AFCD là hình bình hành
b: EG//AB
AB\(\perp\)AC
Do đó: EG\(\perp\)AC
c:
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)

{AD // BCAD = BC AB = CDAB // CD
Vì AD // BC
⇒ AD // BE
Vì {AD = BCBE= BC
⇒ AD = BE
Tứ giác EADB có
{AD // BEAD = BE
⇒ Tứ giác EADB là hình bình hành (đpcm)
b, Vì tứ giác EADB là hình bình hành
⇒ AE // BD (1)
Vì {AB = CDDF = CD
⇒ AB = DF
Vì AB // CD
⇒ AB // DF
Tứ giác ABDF có
{AB = DFAB // DF
⇒ Tứ giác ABDF là hình bình hành
⇒ AF // BD (2)
Từ (1), (2) ⇒ E, A và F thẳng hàng (đpcm)
c, Vì tứ giác EADB là hình bình hành
⇒ AE = BD (3)
Vì tứ giác ABDF là hình bình hành
⇒ AF = BD (4)
Từ (3), (4) ⇒ AE = AF
Vì {AE = AFE, A, F thẳng hàng
⇒ A là trung điểm của EF
⇒ CA là đường trung tuyến của ΔCEF
Vì DC = DF
⇒ D là trung điểm của EF
⇒ ED là đường trung tuyến của ΔCEF
Vì BE = BC
⇒ B là trung điểm của EC
⇒ FB là đường trung tuyến của ΔCEF
Như vậy
{CA là đường trung tuyến của ΔCEF ED là đường trung tuyến của ΔCEFFB là đường trung tuyến của ΔCEF

a: ΔBEK vuông tại E có góc EBK=45 độ
nên ΔEBK vuông cân tại E
=>EK=BE=CF
Xét tứ giác EKFC có
EK//FC
EK=FC
=>EKFC là hình bình hành