Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
=>BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CD và BD//CH
BH//CD
CA\(\perp\)BH
Do đó: \(CA\perp\)CD
=>ΔACD vuông tại C
BD//CH
AB\(\perp\)CH
Do đó: AB\(\perp\)BD
=>ΔABD vuông tại B
c: ΔBAD vuông tại B
mà BI là đường trung tuyến
nên IB=IA=ID(1)
ΔCAD vuông tại C
mà CI là đường trung tuyến
nên CI=IA=ID(2)
Từ (1) và (2) suy ra IA=IB=IC=ID
a) Chứng minh tứ giác BHCD là hình bình hành:
Xét tứ giác BHCD:
M là trung điểm của BC (gt)
M là trung điểm của HD (gt)
*Nên hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường.
* Vậy tứ giác BHCD là hình bình hành (dấu hiệu nhận biết hình bình hành: hai đường chéo cắt nhau tại trung điểm mỗi đường).
b) Chứng minh tam giác ABD vuông tại B và tam giác ACD vuông tại C:
Xét hình bình hành BHCD:
BH // CD (tính chất hình bình hành)
CH // BD (tính chất hình bình hành)
Xét tam giác ABC:
* AF là đường cao (gt) => AF vuông góc với BC
* Mà BH // CD (cmt) => AF vuông góc với CD
Tương tự:
CH // BD (cmt) => AF vuông góc với BD
Kết luận:
* Tam giác ABD vuông tại B (AF vuông góc với BD)
* Tam giác ACD vuông tại C (AF vuông góc với CD)
**c) Chứng minh IA=IB=IC=ID:**
* **Xét tam giác AHD:**
* M là trung điểm của HD (gt)
* I là trung điểm của AD (gt)
* Nên IM là đường trung tuyến của tam giác AHD
* Vậy IA = ID (tính chất đường trung tuyến trong tam giác)
* **Xét tam giác BCD:**
* M là trung điểm của BC (gt)
* I là trung điểm của AD (gt)
* Nên IM là đường trung tuyến của tam giác BCD
* Vậy IB = IC (tính chất đường trung tuyến trong tam giác)
* **Kết luận:**
* IA = IB = IC = ID
**Tóm lại:**
* Tứ giác BHCD là hình bình hành.
* Tam giác ABD vuông tại B và tam giác ACD vuông tại C.
* IA = IB = IC = ID.

a: Xét tứ giác BECM có
D là trung điểm của đường chéo BC
D là trung điểm của đường chéo ME
Do đó: BECM là hình bình hành
Suy ra: BM//EC và BM=EC
mà AE=EC
nên BM//AE và BM=AE
Xét tứ giác AEMB có
AE//BM
AE=MB
Do đó: AEMB là hình bình hành
b: Ta có: AEMB là hình bình hành
nên Hai đường chéo AM và BE cắt nhau tại trung điểm của mỗi đường
Suy ra: O là trung điểm chung của AM và BE
Xét ΔMAE có
D là trung điểm của ME
O là trung điểm của AM
Do đó: DO là đường trung bình của ΔMAE
Suy ra: DO//AE

a: Xét tứ giác ABCD có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo BD
Do đó: ABCD là hình bình hành
b: Xét tứ giác AKCH có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo KH
Do đó: AKCH là hình bình hành
Suy ra: AK=HC

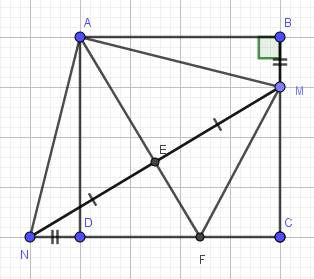
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
a: Xét tứ giác BGCN có
D là trung điểm của đường chéo BC
D là trung điểm của đường chéo GN
Do đó: BGCN là hình bình hành