Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~

Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
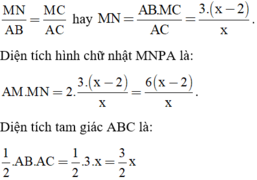
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
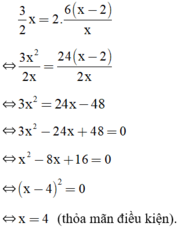
Vậy độ dài đoạn thẳng AC là 4cm.


a)
ta có G là trọng tâm của tam giác ABC.
\(\hept{\begin{cases}\Rightarrow BH=GH=GD\\\Rightarrow EG=GK=KC\end{cases}}\)
hay G là trung điểm của EK và HD.
tứ giác EDKH có 2 đường chéo cắt nhau tại trung điểm mỗi đường
do đó tứ giác EDKH là hình bình hành.
b) để hình bình hành EDKH là hình chữ nhật thì EK=HD
⇒BD=EC⇒ΔABCcân
vậy để hình bình hành EDKH là hình chữ nhật thì tam giác ABC cân
c) vẽ đường cao AI vuông góc với BC.
khi đó AI cũng là đường trung tuyến.
\(\Rightarrow AG=\frac{2}{3}AI\)
ta có :\(\hept{\begin{cases}BE=AE\\AD=DC\end{cases}}\) nên ED là đường trung bình của tam giác ABC.
⇒\(\hept{\begin{cases}ED//BC\\2ED=BC\end{cases}}\)
vì ED//BC và AI⊥BC nên ED⊥AI
đồng thời EH⊥ED nên EH//AI.
ta có: \(\hept{\begin{cases}EH//AI\\BE=EA\end{cases}}\)\(\Rightarrow AH=\frac{AG}{2}\)
hay \(EH=\frac{\frac{2}{3}AI}{2}=\frac{1}{3}AI\Leftrightarrow3EH=AI\)
\(S\Delta ABC=\frac{AI.BC}{2}=\frac{3EH.2ED}{2}=3EH.ED\)=\(3S_{EDHK}\)
vậy\(\frac{S_{EDHK}}{S_{\Delta ABC}}=\frac{1}{3}\)
CHÚC BẠN HỌC TỐT

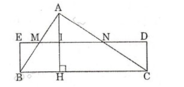
Cho ΔABC với đường cao AH.
Gọi M, N, I là trung điểm của AB, AC, AH.
Lấy E đối xứng với I qua M, D đối xứng với I qua N.
⇒ Hình chữ nhật BEDC là hình cần dựng.
Thật vậy:
Ta có ΔEBM = ΔIAM và ΔDCN = ΔIAN
⇒ SEBM = SAMI và SCND = SAIN
⇒ SABC = SAMI + SAIN + SBMNC = SEBM + SBMNC + SCND = SBCDE.
Suy ra SABC = SBCDE = BE.BC = 1/2.AH.BC. (Vì BE = IA = AH/2).
Ta đã tìm lại công thức tính diện tích tam giác bằng một phương pháp khác

Cho tam giác ABC với đường cao AH. Ta dựng hình chữ nhật có một cạnh bằng một cạnh của tam giác ABC và có diện tích bằng diện tích tam giác ABC như hình dưới
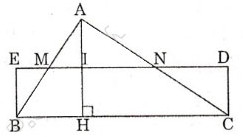
Ta có ∆EBM = ∆KAM và ∆DCN = ∆ KAN
Suy ra
SBCDE = SABC=  BC. AH
BC. AH
Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác.

Đáp án B
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
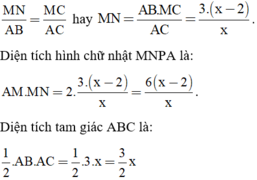
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
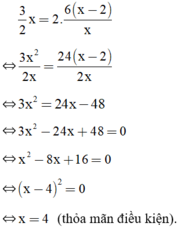
Vậy độ dài đoạn thẳng AC là 4cm.

Bài 1:
Chiều dài là 26x9/13=18(m)
Chiều rộng là 26-18=8(m)
Diện tích là 18x8=144(m2)
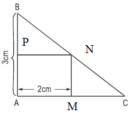
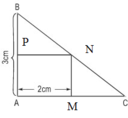
Giả sử ta có tam giác ABC, cần dựng hình chữ nhật có 1 cạnh = cạnh AC của tam giác
Dựng đường cao AH, Trên nửa mặt phảng bờ BC không chưa A Từ B dựng nửa đường thẳng Bx // AH, trên Bx lấy điểm E sao cho BE = AH, Trên nửa mặt phảng bờ BC không chưa A Từ C dựng nửa đường thẳng Cy // AH, trên Cy lấy điểm D sao cho CD = AH
Nối DE ta có Hình CN BCDE có diện tích = diện tích tam giác ABC
Sorry!!!!
BE =BC = 1/2 AH