Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO

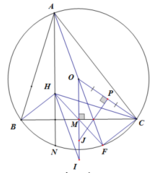
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2
Gọi G là trọng tâm của \(\Delta\)ABC. Từ A kẻ đường kính AK của (O), nối K vs B &C
2 đoạn AM và ON gặp nhau ở điểm I.
Xét đường tròn (O) có đường kính AK, 2 điểm B & C cùng thuộc đường tròn (O)
=> AB vuông BK và AC vuông CK. Mà CH vuông A; BH vuông AC
=> BH//CK; CH//BK (Quan hệ //, vuông góc) => Tứ giác BHCK là hình bình hành.
Ta có M là trung điểm đường chéo BC của hbh BHCK => M là trung điểm HK
Xét \(\Delta\)AKH: O là trung điểm AK; M là trung điểm HK => OM là đường trung bình \(\Delta\)AKH
=> OM//AH và OM=1/2.AH. Lại có: AN=NH=1/2.AH => OM//AN và OM=AN
=> Tứ giác AOMN là hbh. Do I là giao điểm 2 đg chéo nên I là trung điểm ON và AM
=> MI là trung tuyến \(\Delta\)OMN
Ta thấy: G là trọng tâm \(\Delta\)ABC => MG=1/3.AM. Mà AM=2.MI
=> MG=1/3.2.MI=2/3.MI. Xét \(\Delta\)OMN có: Trung tuyến MI, điểm G thuộc MI
Và MG=2/3.MI (cmt) => G là trọng tâm của \(\Delta\)OMN. Mà G cũng là trọng tâm \(\Delta\)ABC
=> 2 tam giác ABC và OMN có chung 1 trọng tâm G (đpcm).