Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: I nằm trên đường trung trực của BC(gt)
nên IB=IC(Tính chất đường trung trực của một đoạn thẳng)

Bạn tự vẽ hình nhé. Mình giải thôi.
1)Bạn chia 2 TH.
a) Góc MDB lớn hơn hoac bằng 60 độ
=>MD<MB mà ME>MC=MB
=>MD<ME.
b) Góc MDB nhỏ hơn 60 độ.
=> MD giao CA tại E .
Dễ dàng cminh DM<ME.
2) Ta có tam giác ABC cân tại A => AI là phân giác cũng là trung trực BC
=> AI trung trực BC. Mà AO là trung trục BC.
=> AI trùng AO.
=>OI là trung trực BC
Đè bài cần xem lại nhé.
3)Ta có góc B > góc C => AC>AB
Có AC đối dienj góc vuông trong tam giác vuông AEC => AC>CE
Tương tự AB>BD
Tất cả các điều => AC-AB>CE-BD

a)
Ta có:
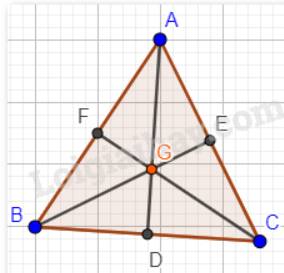
G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);
H là trực tâm của tam giác ABC (giao điểm của ba đường cao);
I là giao điểm của ba đường phân giác của tam giác ABC;
O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).
Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.
Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.
b)
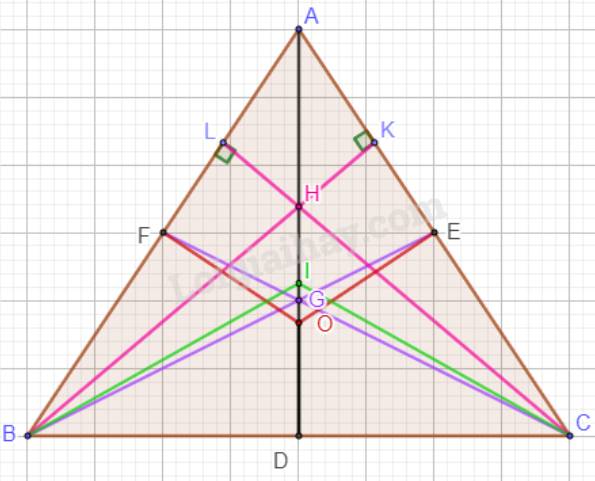
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).
Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.

a)
Trong tam giác ABC cân tại A có AD là đường trung tuyến.
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân);
AD chung;
BD = DC (D là trung điểm của BC).
Vậy \(\Delta ABD = \Delta ACD\)(c.c.c.). Suy ra: \(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (vì ba điểm B, D, C thẳng hàng); \(\widehat {BAD} = \widehat {CAD}\).
Vậy AD là đường cao của tam giác và đường phân giác của góc A.
Suy ra: AD là đường trung trực của tam giác ABC.
Vậy AD là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác ABC.
Mà G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực nên A, G, H, I, O cùng nằm trên một đường thẳng.
Vậy nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.
b)
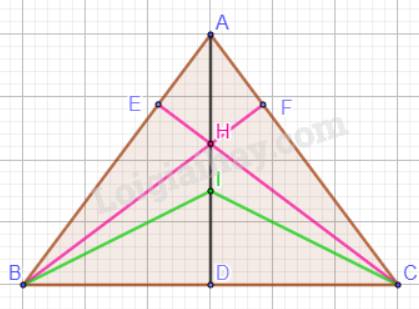
Ta có: \(AD \bot BC\).
H là trực tâm của tam giác ABC nên A, H, D thẳng hàng.
Mà A, H, I thẳng hàng nên A, H, I, K thẳng hàng.
Suy ra: AD là tia phân giác của góc BAC (Vì AI là tia phân giác của góc BAC).
Nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác BAD và tam giác CAD có:
\(\widehat {BAD} = \widehat {CAD}\);
AD chung;
\(\widehat {ADB} = \widehat {ADC}\) (\(AD \bot BC\)).
\(\Rightarrow \Delta ABD = \Delta ACD\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng).
Do đó, tam giác ABC cân tại A
Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.

tự kẻ hình nha:333
a) vì AB là trung trực của DM=> MH=HD( đặt H là giao điểm của AB và DM)
xét tam giác MAB và tam giác DAB có
MH=HD(cmt)
AHM=AHD(=90 độ)
AH chung
=> tam giác MAB= tam giác DAB(cgc)
=> AM=AD( hai cạnh tương ứng)
vì AC là trung trực của DN=> NK=DK( đặt K là giao điểm của AC và DN)
xét tam giác AKD và tam giác AKN có
DK=NK(cmt)
AKD=AKN(=90 độ)
AK chung
=> tam giác AKD= tam giác AKN( cgc)
=> AN=AD ( hai cạnh tương ứng)
AM=AD(cmt)
=> AM=AN=> tam giác AMN cân A
b) vì E thuộc đường trung trực AB=> EM=ED
vì F thuộc đường trung trực AC=> FD=FN
ta có MN=ME+EF+FN mà EM=ED, FD=FN
=> MN= ED+EF+FD
c) xét tam giác ADF và tam giác ANF có
FD=FN(cmt)
AD=AN(cmt)
AF chung
=> tam giác ADF= tam giác ANF(ccc)
=> ANF=ADF( hai góc tương ứng)
xét tam giác AME và tam giác ADE có
AM=AD(cmt)
AE chung
EM=ED(cmt)
=> tam giác AME= tam giác ADE(ccc)
=> AME=ADE( hai góc tương ứng)
mà AME=ANF( tam giác AMN cân A)
=> ADE=ADF=> AD là p/g của EDF
d) chưa nghĩ đc :)))))))