Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: ΔDBC vuông tại D(BD⊥AC tại D)
mà DO là đường trung tuyến ứng với cạnh huyền BC(O là trung điểm của BC)
nên \(DO=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

a Xét tứ giác ABCM có
D là trung điểm chun của AC và BM
=>ABCM là hình bình hành
=>AM//BC và AM=BC
b: Xét tứ giác ANBC có
E là trung điểm chung của AN và BC
=>ANBC là hình bình hành
=>AN//BC và AN=BC
=>M,A,N thẳng hàng

a: Xét ΔADE có
AB/BD=AC/CE
nên BC//DE
b: Xét ΔDBM vuông tại M và ΔECN vuông tại N có
DB=EC
\(\widehat{DBM}=\widehat{ECN}\)
Do đó: ΔDBM=ΔECN
Suy ra: DM=EN
c: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO đó: ΔABM=ΔACN
Suy ra: AM=AN
hay ΔAMN cân tại A

Lời giải:
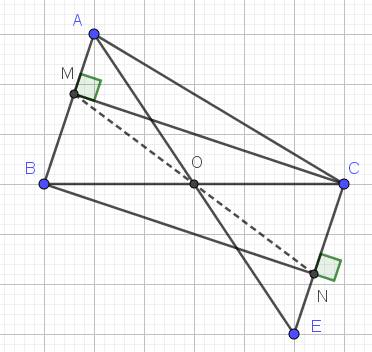
a. Xét tam giác $AOB$ và $EOC$ có:
$\widehat{AOB}=\widehat{EOC}$ (đối đỉnh)
$AO=EO$ (gt)
$OB=OC$ (do $O$ là trung điểm $BC$)
$\Rightarrow \triangle AOB=\triangle EOC$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra:
$AB=EC$ (đpcm)
$\widehat{OAB}=\widehat{OEC}$. Mà 2 góc này ở vị trí so le trong nên $AB\parallel CE$ (đpcm)
c.
Xét tam giác $BMC$ và $CNB$ có:
$\widehat{BMC}=\widehat{CNB}=90^0$
$BC$ chung
$\widehat{MBC}=\widehat{NCB}$ (so le trong)
$\Rightarrow \triangle BMC=\triangle CNB$ (g.c.g)
$\Rightarrow BM=NC$
Xét tam giác $BMO$ và $CNO$ có:
$BM=CN$ (cmt)
$\widehat{MBO}=\widehat{NCO}$ (so le trong)
$BO=CO$
$\Rightarrow \triangle BMO=\triangle CNO$ (c.g.c)
$\Rightarrow \widehat{BOM}=\widehat{CON}$
$\Rightarrow \widehat{BOM}+\widehat{BON}=\widehat{CON}+\widehat{BON}$
$\Rightarrow \widehat{MON}=\widehat{BOC}=180^0$
$\Rightarrow M, O, N$ thẳng hàng.

a: Xét tứ giác ABCE có
D là trung điểm của AC
D là trung điểm của BE
Do đó: ABCE là hình bình hành
Suy ra: AE//BC
a: Ta có: ΔBDC vuông tại D
mà DO là đường trung tuyến
nên DO=BC/2