Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời:
a.
Xét ΔMAB và ΔMDC, ta có:
AM = MD(gt)
BM = MC (gt)
góc BMA = góc DMC (đối đỉnh)
=> ΔMAB = ΔMDC (c.g.c)
b.
Vì ΔMAB = ΔMDC (cmt)
=> AB = DC (2 cạnh tương ứng)
và góc ABM = góc DCM (2 góc tương ứng)
mà góc ABM so le trong với góc DCM
=> AB //DC (đcpcm)
c.
Xét ΔABC và ΔDBC, ta có:
BA = DC (cmt)
BC chung (gt)
góc ABC = góc DCB (cmt)
=> ΔABC = ΔDBC (c.g.c)
d.(mk ko bt thông cảm nha )
Hok Tốt !
# mui #

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: BA=DC; AC=DB
Xét ΔBAC và ΔCDB có
BA=CD
AC=DB
BC chung
Do đó: ΔBAC=ΔCDB
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó: AEDF là hình bình hành
Suy ra: AD và FE cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng

a) Xét \(\Delta MAB\)và \(\Delta MDC\)có:
MA = MD (gt)
\(\widehat{BMA}=\widehat{CMD}\)(2 góc đối đỉnh)
MB = MC (gt)
\(\Rightarrow\Delta MAB=\Delta MDC\left(c-g-c\right)\)
\(\Rightarrow AB=DC\)(2 cạnh tương ứng)
\(\widehat{BAM}=\widehat{CDM}\)(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
b) Xét \(\Delta ACM\)và \(\Delta DBM\)có:
MA = MD (gt)
\(\widehat{AMC}=\widehat{BMD}\)(2 góc đối đỉnh)
MB = MC (gt)
\(\Rightarrow\Delta ACM=\Delta DBM\left(c-g-c\right)\)
\(\Rightarrow AC=DB\)(2 cạnh tương ứng)
Xét \(\Delta BAC\)và \(\Delta CDB\)có:
AB = DC (cmt)
AC = DB (cmt)
BC là cạnh chung
\(\Rightarrow\Delta BAC=\Delta CDB\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAC}=\widehat{CDB}\)(2 góc tương ứng)
c) Bn tự lm nhá!! Phần này mk chưa nghĩ ra. Tốn chất xám lắm!!!!!

a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>BD//CA
c: Xét ΔABC và ΔDCB có
AB=DC
BC chung
AC=DB
=>ΔABC=ΔDCB
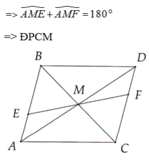
d: Xét tứ giác AEDF có
AE//DF
AE=DF
=>AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>E,M,F thẳng hàng

a, xét tam giác MAB và tam giác MDC có :
MB = MC do M là trđ của BC (gt)
MD = MA (GT)
góc BMA = góc DMC (Đối đỉnh)
=> tam giác MAB = tam giác MDC (c-g-c)
b, tam giác MAB = tam giác MDC (Câu a)
=> AB = DC (đn)
và góc BAM = góc MDC (đn) mà 2 góc này slt
=> AB // DC (Đl)
c, AB // DC (Câu b)
=> góc ABC = góc BCD (slt)
xét tam giác ABC và tam giác DCB có : BC chung
AB = DC (câu b)
=> tam giác ABC = tam giác DCB (c-g-c)
=> góc BAC = góc CDB (đn)

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//DC và AB=DC
c: Ta có: ABDC là hình bình hành
nên \(\widehat{BAC}=\widehat{BDC}\)