Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cosB=(16^2+BC^2-14^2)/(2*16*BC)
=>BC^2+60=32*BC*cos40
=>BC=21,76cm
S ABC=1/2*21,76*16*sin40=111,90cm2

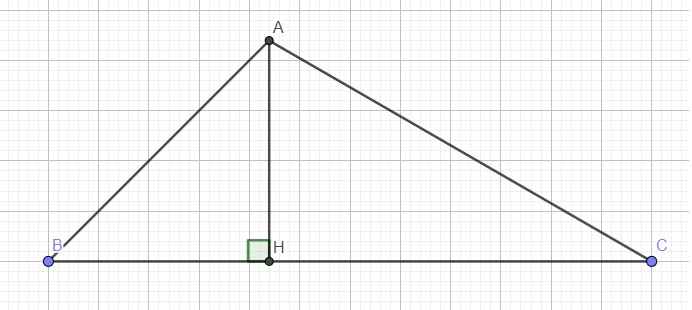
Kẻ đường cao AH
Trong tam giác vuông ABH:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{BC^2}{cotB+cotC}=\dfrac{1}{2}.\dfrac{6^2}{cot45^0+cot30^0}\approx11,4\left(cm^2\right)\)

\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
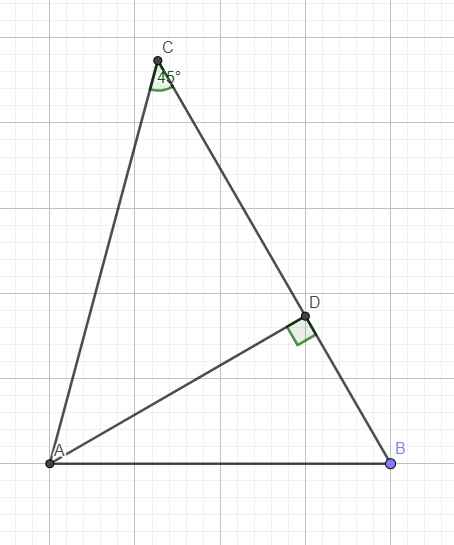
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)

Đồng chí tự vẽ hình nhé.
Kẻ \(AD\perp BC=\left\{D\right\}\)
a, \(\Delta ABD\)có: \(\widehat{ADB}=90^o\)
\(\Rightarrow AD=AB.\sin B\Leftrightarrow AD=16.\sin30=8\sqrt{3}\left(cm\right)\)
\(\Delta ABD\)có: \(\widehat{ADB}=90^o\)
\(\Rightarrow AB^2=AD^2+BD^2\)(định lý Py-ta-go)
hay \(16^2=\left(8\sqrt{3}\right)^2+BD^2\)
\(BD^2=64\)
\(BD=8\left(cm\right)\)
\(\Delta ADC\)có: \(\widehat{ADC}=90^o\)
\(\Rightarrow AC^2=AD^2+CD^2\)(định lý Py-ta-go)
hay \(14^2=\left(8\sqrt{3}\right)^2+CD^2\)
\(CD^2=4\)
\(CD=2\left(cm\right)\)
Ta có: \(BC=CD+BD=2+8=10\left(cm\right)\)
b, \(S_{\Delta ABC}=\frac{AD.BC}{2}=\frac{8\sqrt{3}.10}{2}=40\sqrt{3}\left(cm^2\right)\)
Thật sự tui không biết mình có làm đúng không, sai thì nhớ bảo nhá

làm ơn giải hộ mình đi mà
còn cần giải nữa ko