Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Tính BC
tam giác ABC vuông tại A
Theo pitago ta có BC2=AB2+AC2
Mà AB=8
AC=6
=>BC2=64+36=100
=>BC=10
b,Tam giác BAI=tamgiác KAI(c.g.c)=>BI=KI
Góc BIA= góc KIA
Góc BIA+ gócBIC=1800
GócKIA+ góc KIC=1800
Mà góc BIA= góc KIA
=>Góc BIC = góc KIC
Xét tam giác BIC và tam giác KIC có
BI = KI(cmt)
GócBIC = góc KIC(cmt)
IC cạnh chung
=>tam giác BIC= tam giác KIC(c.g.c)
c, d, Tớ hết thời gian rồi k tớ nhé

Hình tự vẽ ( vẽ ở đây hơi khó )
a,Tam giác ABC cân tại A
=> \(\widehat{BAC}=180^o-2\widehat{ACB}^{\left(1\right)}\)
Tam giác IAC cân tại I ( tự chứng minh tam giác IAM = tam giác IMC )
=>\(\widehat{AIC}=180^o-2\widehat{ACB}^{\left(2\right)}\)
Từ (1)(2) => \(\widehat{BAC}=\widehat{AIC}\)
b,\(\widehat{IBA}=\widehat{BAC}+\widehat{ACB}\)(t/c góc ngoài của tam giác)
\(\widehat{KAC}=\widehat{AIC}+\widehat{ACB}\) (t/c góc ngoài của tam giác)
mà \(\widehat{BAC}=\widehat{AIC}\left(cmt\right)\)
\(\Rightarrow\widehat{IBA}=\widehat{KAC}\)
Xét tam giác KAC và tam giác IBA có :
KA = IB (gt)
góc IBA = góc KAC (cmt)
AC = BA(gt)
=> tam giác KAC = tam giác IBA (c.g.c)
=> AI=KC (2 cạnh tương ứng)
mà AI = IC => KC=IC
c,CI = CK (câu b) => tam giác CIK cân tại C
Do đó góc ICK = 90o <=> góc K = góc AIC =45o
<=> góc BAC = 45o ( vì góc AIC = góc BAC (câu a))
Vậy tam giác ABC có AB=AC ,AB>BC và góc BAC = 45o thì góc ICK = 90o
d, Đang nghĩ :(
Làm tiếp câu D
\(S_{\Delta ICK}=S_{\Delta ABC}+S_{\Delta AIB}+S_{\Delta AKC}=S_{\Delta ABC}+2_{\Delta AIB}\) (Vì \(\Delta AIB=\Delta AKC\))
Mà \(S_{\Delta AIC}=3S_{\Delta ABC}\Rightarrow3S_{\Delta ABC}=S_{\Delta ABC}+2S_{\Delta AIB}\Rightarrow S_{\Delta ABC}=S_{\Delta AIB}\)
\(\Rightarrow IB=BC\)( vì chung chiều cao kẻ từ A)
Mà AB cắt IM tại H -> H là trọng tâm của tam giác AIC
-> CH đi qua trung điểm của AI
P/s: Bài này bn nên vẽ hai hình

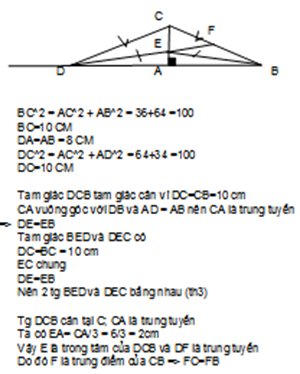
Đáp án:
a) Vì ΔΔABC vuông tại A (Aˆ=90oA^=90o)
=> AB2+AC2=BC2AB2+AC2=BC2 (ĐL Pi-ta-go)
=> BC2=82+62=100BC2=82+62=100
=> BC=10BC=10cm
b) Vì AB = AD (gt)
mà A ∈∈ BD (gt)
=> A trung điểm BD (ĐN trung điểm)
=> CA trung tuyến BD (ĐN trung tuyến)
lại có: CA ⊥⊥ BD (AB ⊥⊥ AC do Aˆ=90oA^=90o)
=> ΔΔCBD cân tại C (dhnb)
=> BC = CD (ĐN ΔΔ cân)
và CA là phân giác của BCDˆBCD^ (t/c ΔΔ cân)
=> C1ˆ=C2ˆC1^=C2^ (ĐN tia p/g)
Xét ΔΔBEC và ΔΔDEC có:
BC = CD (cmt)
C1ˆ=C2ˆC1^=C2^ (cmt)
EC: cạnh chung
=> ΔΔBEC = ΔΔDEC (c.g.c)
c) Vì CE là trung tuyến của ΔΔBCD (cmt)
mà AEAC=26=13AEAC=26=13 (AE = 2cm, AC = 6cm)
=> E là trọng tâm ΔΔBCD (dhnb)
=> DE là trung tuyến ΔΔBCD (ĐN trọng tâm)
=> DE đi qua trung điểm của BC (ĐN trung tuyến)

Dễ mà p áp dụng Pytago câu a, còn mấy câu kia mìh lm` biến vẽ hìh Cm qá p ơi.

Bài 12:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=8^2+6^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD(gt)
Do đó: ΔABC=ΔADC(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔEAB vuông tại A và ΔEAD vuông tại A có
EA chung
AB=AD(gt)
Do đó: ΔEAB=ΔEAD(hai cạnh góc vuông)
Suy ra: EB=ED(hai cạnh tương ứng)
Xét ΔCEB và ΔCED có
CE chung
CB=CD(cmt)
EB=ED(cmt)
Do đó: ΔCEB=ΔCED(c-c-c)
cần giải câu c thôi