Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔADB vuông tại D
=>D,A,B cùng nằm trên đường tròn đường kính AB(1)
Ta có: ΔEAB vuông tại E
=>E,A,B cùng nằm trên đường tròn đường kính AB(2)
Từ (1),(2) suy ra D,A,E,B cùng thuộc một đường tròn
b: Ta có: ΔADC vuông tại D
=>D nằm trên đường tròn đường kính AC(3)
Ta có: ΔCFA vuông tại F
=>F nằm trên đường tròn đường kính AC(4)
Từ (3) và (4) suy ra C,F,A,D cùng thuộc một đường tròn
c: Ta có:ΔCEB vuông tại E
=>E nằm trên đường tròn đường kính CB(5)
ta có: ΔCFB vuông tại F
=>F nằm trên đường tròn đường kính CB(6)
Từ (5),(6) suy ra B,C,F,E cùng thuộc một đường tròn

a, Gọi I là trung điểm AB
Xét tam giác AEB vuông tại E, I là trung điểm
=> \(EI=AI=IB=\frac{AB}{2}\)(1)
Xét tam giác ADB vuông tại D, I là trung điểm
=> \(DI=AI=IB=\frac{AB}{2}\)(2)
Từ (1) ; (2) => A ; D ; B ; F cùng nằm trên đường tròn (I;AB/2)
b, Gọi O là trung điểm AC
Xét tam giác AFC vuông tại F, O là trung điểm
=> \(FO=AO=CO=\frac{AC}{2}\)(3)
Xét tam giác CDA vuông tại D, O là trung điểm
=> \(DO=AO=CO=\frac{AC}{2}\)(4)
Từ (3) ; (4) => A ; D ; C ; F cùng nằm trên đường tròn (O;AC/2)
c, Gọi T là trung điểm BC
Xét tam giác BFC vuông tại F, T là trung điểm
=> \(FT=BT=CT=\frac{BC}{2}\)(5)
Xét tam giác BEC vuông tại E, T là trung điểm
=> \(ET=BT=CT=\frac{BC}{2}\)(6)
Từ (5) ; (6) => B ; C ; E ; F cùng nằm trên đường tròn (T;BC/2)

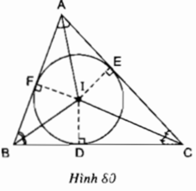
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I

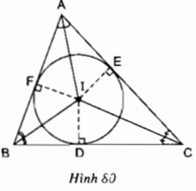
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I

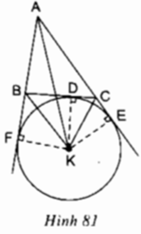
Theo tính chất tia phân giác, ta có:
AK là tia phân giác của góc BAC
⇒ KE = KF
Tương tự: CK là tia phân giác của góc ngoài của góc ACB
⇒ KE = KD
Do đó: KE = KF = KD
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm K

#)Giải :
Bài 1 :
a) Các \(\Delta DBC;\Delta EBC\) nội tiếp đường tròn đường kính BC
\(\Rightarrow\Delta DBC;\Delta EBC\) vuông
\(\Rightarrow CD\perp AB;BE\perp AC\)
b) K là trục tâm của \(\Delta ABC\)
\(\Rightarrow AK\perp BC\)
a: Xét tứ giác ADBE có
\(\widehat{ADB}+\widehat{AEB}=90^0+90^0=180^0\)
nên ADBE là tứ giác nội tiếp
=>A,D,B,E cùng thuộc một đường tròn
b: Xét tứ giác ADCF có
\(\widehat{ADC}+\widehat{AFC}=90^0+90^0=180^0\)
nên ADCF là tứ giác nội tiếp
=>A,D,C,F cùng thuộc một đường tròn
c: Xét tứ giác BEFC có
\(\widehat{BEC}=\widehat{BFC}=90^0\)
=>BEFC là tứ giác nội tiếp
=>B,E,F,C cùng thuộc một đường tròn