Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

SDIE=1/2SAID=8
SBDE=1/2SDEC=2SBIE+16
SABE=1/2SAEC
=>SABI+SBIE=1/2(2SBIE+16+8+16)
=>SABI=20
Mà SABI=2/9SABC
=>SABC=90cm2

Đây là bài toán thuộc dạng chứng minh, bạn hãy nhìn vào hình vẽ.
Bài này thuộc dạng vừa, mình mong bạn có thể làm được.

Hai tam giác ABE và ABC có chung cao hạ từ A xuống BC đáy BE=1/2 EC hay BE = 1/3 EC
Suy ra SABE = 1/3 SABC
Ta có hình vẽ :
Nối IC ta có :
+ dt ABI = 2/3 x dt ABE [Vì đáy AI = 2/3 x AE, chung đường cao kẻ từ B tới AE] 1
+ dt ABE = 1/3 x dt ABC [Vì đáy BE = 1/3 x BC, chung đường cao kẻ từ A tới BC] 2
Từ 1 và 2 ta có : dt ABI = 2/3 x 1/3 x dt ABC
= 2/9 x dt ABC
+ dt IEC = 1/3 x dt AEC [Vì đáy IE = 1/3 x AE, chung đường cao kẻ từ C tới AE] 3
+ dt IBE = 1/3 x dt ABE [Vì đáy IE = 1/3 x AE, chung đường cao kẻ từ B tới AE] 4
Từ 3 và 4 ta có : dt IEC + dt IBE = 1/3 x (dt AEC + dt ABE)
dt IBC = 1/3 x dt ABC
Phân số chỉ tỉ số giữa dt tam giác ABI và dt tam giác IBC là :
2/9 : 1/3 = 2/3 x (dt IBC)
- Vì dt ABI = 2/3 x dt IBC mà 2 hình này có chung đáy BD suy ra đường cao kẻ từ A tới BD = 2/3 đường cao kẻ từ C tới BD hay đường cao kẻ từ A tới ID = 2/3 đường cao kẻ từ C tới ID.
+ dt AID = 2/3 x dt CID [Vì chung đáy ID, đường cao kẻ từ A tới ID = 2/3 đường cao kẻ từ C tới ID]
- Vì dt AID = 2/3 x dt CID mà 2 hình này có chung đường cao kẻ từ I tới AC nêm suy ra đáy AD = 2/3 x DC
+ dt AID = 2/3 x dt IDC [Vì đáy AD = 2/3 x DC, chung đường cao kẻ từ I tới AC]
Diện tích tam giác IDC là : 16 : 2/3 = 24 (cm2)
Diện tích tam giác AIC là : 16 + 24 = 40 (cm2)
+ dt AIC = 2/3 x dt AEC [Vì đáy AI = 2/3 x AE, chung đường cao kẻ từ C tới AE]
Diện tích tam giác AEC là : 40 : 2/3 = 60 (cm2)
+ dt AEC = 2/3 dt ABC [Vì đáý EC = 2/3 x BC, chung đường cao kẻ từ A tới BC]
Diện tích tam giác ABC là : 60 : 2/3 = 90 (cm2)

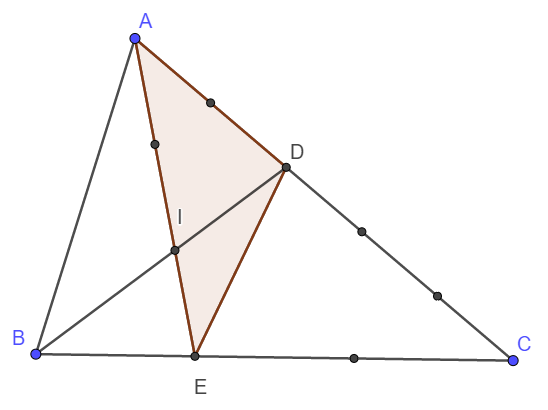
Ta thấy tam giác DAI và tam giác DIE có chung chiều cao, cạnh đáy AI = 2IE nên \(\frac{S_{AID}}{S_{IDE}}=2\)
Tương tự \(\frac{S_{BAI}}{S_{BIE}}=2\)
\(\Rightarrow\frac{S_{DAI}+S_{BAI}}{S_{DIE}+S_{BIE}}=\frac{S_{ADB}}{S_{BED}}=2\)
Lại có \(\frac{S_{DBC}}{S_{BDE}}=3\Rightarrow\frac{S_{ABD}}{S_{DBC}}=\frac{2}{3}\Rightarrow\frac{AD}{DC}=\frac{2}{3}\) (1)
Ta có \(\frac{S_{ADE}}{S_{ABC}}=\frac{S_{ADE}}{S_{AEC}}.\frac{S_{AEC}}{S_{ABC}}=\frac{2}{5}.\frac{2}{3}=\frac{4}{15}\)
\(\frac{S_{ABE}}{S_{ABC}}=\frac{1}{3}\Rightarrow\frac{S_{ADE}}{S_{ABE}}=\frac{4}{5}\)
\(\Rightarrow\frac{ID}{BI}=\frac{4}{5}\)
\(\Rightarrow S_{ABI}=16:4\times5=20\left(cm^2\right)\)
\(\Rightarrow S_{ABD}=16+20=36\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=36:2\times5=90\left(cm^2\right)\)
Bài giải :

Ta thấy tam giác DAI và tam giác DIE có chung chiều cao, cạnh đáy AI = 2IE nên SAIDSIDE =2
Tương tự SBAISBIE =2
⇒SDAI+SBAISDIE+SBIE =SADBSBED =2
Lại có SDBCSBDE =3⇒SABDSDBC =23 ⇒ADDC =23 (1)
Ta có SADESABC =SADESAEC .SAECSABC =25 .23 =415
SABESABC =13 ⇒SADESABE =45
⇒IDBI =45
⇒SABI=16:4×5=20(cm2)
⇒SABD=16+20=36(cm2)
⇒SABC=36:2×5=90(cm2)

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Vũ Thị Hương Giang - Toán lớp 5 - Học toán với OnlineMath

Kết quả bài này là 90 cm2
Giải bài này dài lắm nên mk ko giải ra đc đâu