Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a.
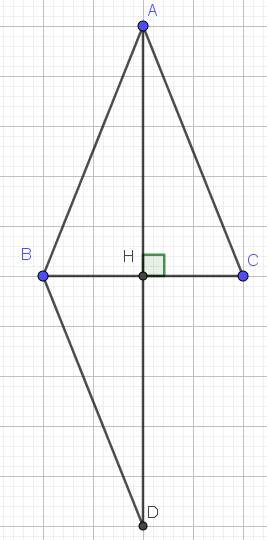
Xét tam giác $ABH$ và $ACH$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$AH$ chung
$\widehat{AHB}=\widehat{AHC}=90^0$
$\Rightarrow \triangle ABH=\triangle ACH$ (ch-cgv)
b.
Do $BD\parallel AC$ nên $\widehat{DBH}=\widehat{HCA}=\widehat{ABH}$ (hai góc so le trong)
Xét tam giác $DBH$ và $ABH$ có:
$BH$ chung
$\widehat{DBH}=\widehat{ABH}$ (cmt)
$\widehat{BHD}=\widehat{BHA}=90^0$
$\Rightarrow \triangle DBH=\triangle ABH$ (g.c.g)
$\Rightarrow DB=AB$ (đpcm)

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng

a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD

a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD

a: Xét ΔABC và ΔCDA có
\(\widehat{ACB}=\widehat{CAD}\)
AC chung
\(\widehat{CAB}=\widehat{ACD}\)
Do đó: ΔABC=ΔCDA
b: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Suy ra: Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
hay M là trung điểm của AC
c: Xét ΔAMI và ΔCMK có
\(\widehat{IAM}=\widehat{KCM}\)
AM=CM
\(\widehat{AMI}=\widehat{CMK}\)
Do đó: ΔAMI=ΔCMK
Suy ra: MI=MK
mà M,I,K thẳng hàng
nên M là trung điểm của IK

a: Xét tứ giác ABED có
ED//AB
AD//BE
=>ABED là hình bình hành
=>AE cắt BD tại trung điểm của mỗi đường
=>IA=IE
b: DI=DB/2=BC/4
=>CD=2DI
=>CD=2/3CI
Xét ΔCAE có
CI là trung tuyến
CD=2/3CI
=>D là trọng tâm
=>A,D,K thẳng hàng



tôi không biết