Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


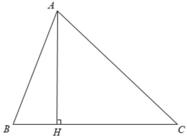
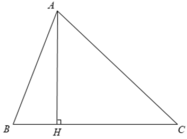
Xét \(\Delta ABH\left(\widehat{AHB}=90^o\right)\) có:
\(AB^2=AH^2+BH^2\) ( theo định lí Py-ta-go)
\(15^2=AH^2+12^2\)
\(\Rightarrow AH^2=81\Rightarrow AH=9\left(cm\right)\)
Xét \(\Delta AHC\left(\widehat{AHC}=90^o\right)\) có:
\(AC^2=AH^2+HC^2\) (theo định lí Py-ta-go)
\(41^2=9^2+HC^2\)
\(\Rightarrow HC^2=1600\Rightarrow HC=40\left(cm\right)\)
Ta có:\(BC=CH+HB=40+12=52\left(cm\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.9.52=234\left(cm^2\right)\)
Áp dụng Pitago có
\(AH^2=AB^2-HB^2\Leftrightarrow AH=\sqrt{15^2-12^2}=9\)
Lại có \(HC^2=AC^2-AH^2\Leftrightarrow HC=\sqrt{41^2-9^2}=40\)
Có BC=HB+HC=12+40=52
Có BC,AH tính S easy

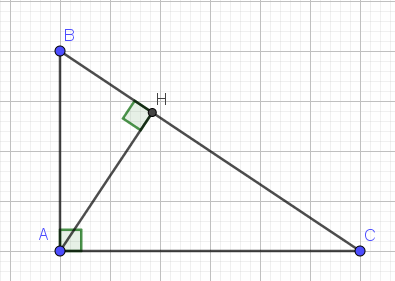
a, Xét tam giác ABH và tam giác CAH ta có :
^AHB = ^CHA = 900
^BAH = ^HCA ( cùng phụ ^HAC )
Vậy tam giác ABH ~ tam giác CAH ( g.g )
b, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác AHB vuông tại H
\(AB^2=BH^2+AH^2\Rightarrow BH^2=AB^2-AH^2=225-144=81\Rightarrow BH=9\)cm
* Áp dụng hệ thức :
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{144}{9}=16\)cm
=> BC = HC + HB = 16 + 9 = 25 cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AC=\dfrac{AH.BC}{AB}=\dfrac{12.25}{15}=20\)cm
a) Xét ΔBHA vuông tại H và ΔAHC vuông tại H có
\(\widehat{BAH}=\widehat{ACH}\left(=90^0-\widehat{B}\right)\)
Do đó: ΔBHA\(\sim\)ΔAHC(g-g)

a.Xét tam giác ANH và tam giác AHC, có:
\(\widehat{ANH}=\widehat{AHC}=90^0\)
\(\widehat{NAH}=\widehat{HCA}\) ( cùng phụ với \(\widehat{A}\) )
Vậy tam giác ANH đồng dạng tam giác AHC ( g.g )
b. Xét tam giác AHB và tam giác ABC, có:
\(\widehat{BAC}=\widehat{AHB}=90^0\)
\(\widehat{B}:chung\)
Vậy tam giác AHB đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{BH}{AB}\)
\(\Leftrightarrow\dfrac{12}{13}=\dfrac{BH}{15}\)
\(\Leftrightarrow13BH=180\)
\(\Leftrightarrow BH=\dfrac{180}{13}cm\)
Xét tam giác AHC và tam giác ABC, có:
\(\widehat{CAB}=\widehat{CHA}=90^0\)
\(\widehat{C}:chung\)
Vậy tam giác AHC đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{CH}{AC}\)
\(\Leftrightarrow\dfrac{12}{15}=\dfrac{CH}{13}\) \(\Leftrightarrow\dfrac{4}{5}=\dfrac{CH}{13}\)
\(\Leftrightarrow5CH=52\)
\(\Leftrightarrow CH=\dfrac{52}{5}cm\)

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

Lời giải:
a. Xét tam giác $AHB$ và $CHA$ có:
$\widehat{AHB}=\widehat{CHA}=90^0$
$\widehat{HAB}=\widehat{HCA}$ (cùng phụ với $\widehat{HAC}$)
$\Rightarrow \triangle AHB\sim \triangle CHA$ (g.g)
b.
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
Từ tam giác đồng dạng phần a suy ra $CH=\frac{AH^2}{BH}=\frac{12^2}{9}=16$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)


Mk tìm các cạnh của tam giác ABC còn bạn tính chu vi hay diện tích thì mk ko biết nha
Áp dụng định lý Py-ta-gô vào tam giác vuông ABH tại H ta có:
\(AH^2+BH^2=AB^2\Rightarrow AH^2=AB^2-HB^2=15^2-12^2=81=9^2\Rightarrow AH=9\)
Tiếp tục áp dụng định lý Py-ta-gô vào tam giác vuông AHC ta có:
\(AH^2+HC^2=AC^2\Rightarrow HC^2=AC^2-AH^2=1600=40^2\Rightarrow HC=40\)
\(\Rightarrow BC=12+40=52\)
ok
Như QQ