Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O

Giả sử M nằm giữa B and D
a)
tam giác IED có:
\(\hept{\begin{cases}IE=ID=\frac{1}{2}AM\\\widehat{EID}=2.\widehat{BAD}=60^0\end{cases}}\)
=> TAM GIÁC IED là tam giác đều (1)
Chứng minh tương tự ta được tam giác IFD là tam giác đều (2).
Từ (1) và (2) suy ra DEIF là hình thoi.
b) Vì
tam giác ABC đều nên trực tâm H củng là trọng tâm. Suy ra:
AH = 2.HD
Gọi P là trung điểm của AH
=> AP = PH = HD. Suy ra IP, KH thứ tự là đường trung bình của các tam giác AMH và DIP
=> MH // IP và KH // IP,
=> M , K , H thẳng hàng
c)
Vì tam giac EDK vuông tại K nên ta có: EF =2.EK = 2. ED.sinKDE =\(\sqrt{3}\).DE do đó EF đạt GTNN
=>DE đạt GTNN => \(DE\perp AB=>M\)trùng zs D ( Có thể dùng đ.lý pitago để tính EF theo DE ).
d) ta có diện tích DEIF=\(\frac{1}{2}DI.EF\)theo DE
e)e) Tìm quỹ tích của K thông qua quỹ tích của I.
bài này dài lắm . nên gợi ý như thế thôi . cần hỏi chỗ nào ib riêng cho mình ^^

Dùng hình của bạn Ngọc nhé
a) \(\Delta ABC\)đều có \(\widehat{BAC}=60^0;\)đường cao AD cũng là phân giác và trực tâm H cũng là trọng tâm
I là trung điểm của cạnh huyền chung AM của các tam giác vuông \(\Delta AEM,\Delta AFM,\Delta ADM\)nên \(IA=IE=ID=IF=\frac{AM}{2}\)(1)
\(\widehat{EIM}\)là góc ngoài của \(\Delta AIE\)cân tại I nên \(\widehat{EIM}=2\widehat{BAM}\). Tương tự, \(\widehat{MID}=2\widehat{MAD};\widehat{MIF}=2\widehat{MAC}\)
\(\widehat{EID}=\widehat{EIM}+\widehat{MID}=2\left(\widehat{BAM}+\widehat{MAD}\right)=2\widehat{BAD}=\widehat{BAC}=60^0\)
\(\widehat{EIF}=\widehat{EIM}+\widehat{MIF}=2\left(\widehat{BAM}+\widehat{MAC}\right)=2.60^0=120^0\)
\(\Rightarrow\widehat{DIF}=120^0-60^0=60^0\)
\(\Delta EDI\)cân tại I có \(\widehat{EID}=60^0\)nên là tam giác đều, suy ra EI = ED (2)
\(\Delta FDI\)cân tại I có \(\widehat{DIF}=60^0\)nên là tam giác đều, suy ra FI = FD (3)
(1),(2),(3) => IE = ED = DF = IF => DEIF là hình thoi
b) Gọi P là trung điểm AH thì \(AP=PH=\frac{AH}{2}=HD\)
Cho ID cắt EF tại K thì K là trung điểm ID (tính chất hình thoi ABCD)
\(\Delta AMH\)có IP là đường trung bình nên IP // MH (4)
\(\Delta DPI\)có KH là đường trung bình nên IP // KH (5)
(4),(5) => M,K,H thẳng hàng. Vậy MH, ID, EF đồng quy tại K

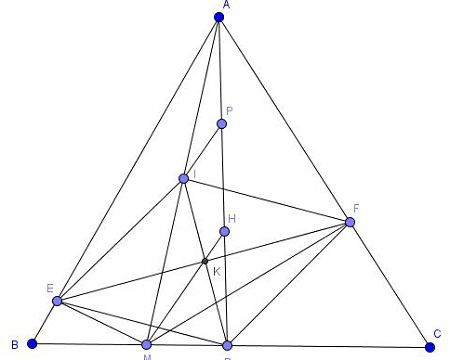
a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O

 Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O
a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O
a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O