Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên \(S_{MEC}=4S_{MAE}=4\times20=80\left(cm^2\right)\)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên \(S_{MBD}=S_{MCD}\)
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên \(S_{EBD}=S_{ECD}\)
Vậy nên \(S_{MBE}=S_{MEC}=80\left(cm^2\right)\)
Ta có \(\frac{S_{AME}}{S_{MEC}}=\frac{1}{4};\frac{S_{ABE}}{S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{AME}+S_{ABE}}{S_{MEC}+S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{MBE}}{S_{MEBC}}=\frac{1}{4}\)
\(\Rightarrow S_{MEBC}=4.80=320\left(cm^2\right)\)
\(\Rightarrow S_{MBC}=320+80=400\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=400-20-80=300\left(cm^2\right)\)

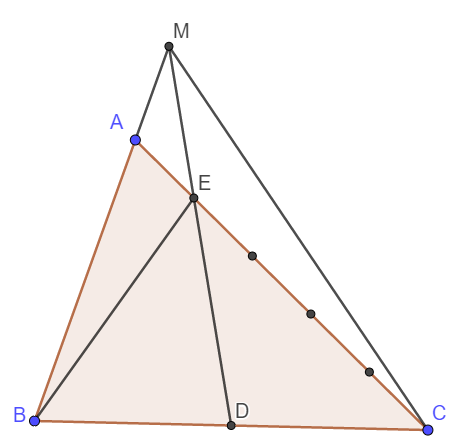
Cho tam giác ABC. Gọi D là điểm chính giữa của cạnh BC. Lấy E trên cạnh AC sao cho AE bằng 1/5 AC. Nối D với E. Kéo dài DE cắt AB kéo dài tại M. Nối M với C. Biết diện tích AME bằng 20 cm2 .Tính diện tích MEC và ABC?
Được cập nhật 22 tháng 5 2019 lúc 20:10
4
![]()
![]()
Hoàng Thị Thu Huyền Quản lý
7 tháng 3 2018 lúc 10:05

a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên SMEC=4SMAE=4×20=80(cm2)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên SMBD=SMCD
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên SEBD=SECD
Vậy nên SMBE=SMEC=80(cm2)

Nối AE, CG ta có:
- = x 2 (vì cùng đường cao hạ từ G xuống AC và đáy AD = CD x 2).
- Mà = x 2 (cùng đườ


Vì D,E là trung điểm của 2 cạnh AB,AC =>BE và CD là 2 đường trung tuyến tam giác ABC.
Mà BE và CD cắt nhau tại M =>M là trọng tâm tam giác ABC
=> AN là trung tuyến tam giác ABC
Hay N là trung điểm của BC.

Từ E kẻ đt // cắt DN ở H
Từ B kẻ đt // cắt DN ở K
+ Có: DN//=1/2 ME (DN là đường trung bình tg CME)
MD// EH (theo ta kẻ)
=> MDHE là hbh
=> ME=DH
mà DN=1/2ME
=> NH=ND
+ Xét tg NBK:
E là trung điểm BN
EH//BK (cùng //AC theo tc hbh và ta kẻ)
=> EH là đường trung bình tg NBK
=> KH=HN
=> KH=HN=ND=1/3 AB=2cm
+ Lại có:
AD//BK (ta kẻ)
AD=2 MD (M là tđiểm AD)
BK=2 EH (tc đường tb tg)
=> AD//=BK
=> ADKB là hbh
=> DK//AB
=> GBE= góc DNE (so le trong) (3)
Từ (1), (2), (3)=> tg BEG=tg NED (gcg)
=> BG=DN=2 cm (đpcm).
Ta có : DC/CA = CM/CB = DM/AB = 1/3 (vì AD = 2DC ; BE = 1/2 EC)(*).
(*)=> DM = AB/3 = 6/3 = 2 (cm)
(*)=> góc CDM = góc CAB ( định lý ta-lét đảo )
<=> CDM + góc C = góc CAB + góc C
<=> góc DME = góc EBG (1)
ME =EB (=CB/3) (2)
góc DEM = góc BEG ( đối đỉnh ) (3)
Từ 1,2,3 => tam giác EDM = tam giác EGB (g.c.g)
Nên : BG = DM = 2 (cm)
tk cho mk nha $_$
Vì D,E,M thẳng hàng nên ta có: \(\dfrac{DB}{DC}\times\dfrac{EC}{EA}\times\dfrac{MA}{MB}=1\)
=>\(\dfrac{MA}{MB}\times2\times1=1\)
=>\(\dfrac{MA}{MB}=\dfrac{1}{2}\)
=>A là trung điểm của MB
=>AM=AB