Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, từ A=90°+B
->B=90°_A
Xét Tam giác AHC vuông tại H
ACH=90°-A
->B=ACH


a) (g.g) suy ra hay (1)
Chứng minh tương tự:
(g.g) suy ra hay (2)
Mà (g.g) suy ra hay (3)
Từ (1), (2) và (3) ta có suy ra .
b) Vì suy ra
Trong tam giác vuông tại nên
Trong tam giác vuông tại có suy ra .
Do đó, (c.g.c).
suy ra .
Vậy cm.

\(BE||DM\) (cùng vuông góc AC)
Theo định lý Talet: \(\left\{{}\begin{matrix}\dfrac{MK}{EH}=\dfrac{CK}{CH}\\\dfrac{DK}{BH}=\dfrac{CK}{CH}\end{matrix}\right.\) \(\Rightarrow\dfrac{MK}{EH}=\dfrac{DK}{BH}\)
\(\Rightarrow\dfrac{BH}{EH}=\dfrac{DK}{MK}\)
Hai tam giác vuông AHE và ACD đồng dạng (chung góc A) \(\Rightarrow\dfrac{AH}{AC}=\dfrac{AE}{AD}\Rightarrow AH.AD=AC.AE\)
Tương tự CHE đồng dạng CAF \(\Rightarrow\dfrac{CH}{AC}=\dfrac{CE}{CF}\Rightarrow CH.CF=AC.CE\)
\(\Rightarrow AH.AD+CH.CF=AC.AE+AC.CE=AC\left(AE+CE\right)=AC^2\) (1)
Lại có 2 tam giác vuông ACD và DCM đồng dạng (chung góc C)
\(\Rightarrow\dfrac{AC}{CD}=\dfrac{CD}{CM}\Rightarrow AC=\dfrac{CD^2}{CM}\Rightarrow AC^2=\dfrac{CD^4}{CM^2}\) (2)
(1); (2) suy ra đpcm

Hình gửi kèm
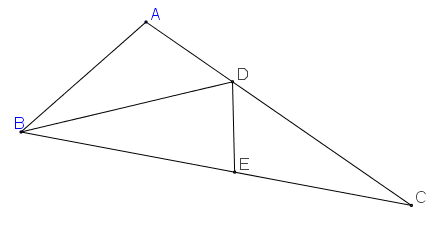 Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/
Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/
