Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M H
Từ A kẻ đường thẳng AH vuông góc với BC ( H thuộc BC )
Ta có : \(S_{ABM}=\frac{1}{2}\cdot BM\cdot AH\)(1)
và \(S_{ACM}=\frac{1}{2}\cdot MC\cdot AH\)(2)
Mặt khác ta có AM là đường trung tuyến
=> \(BM=MC\)(3)
Từ (1), (2) và (3) ta có : \(S_{ABM}=S_{ACM}\left(đpcm\right)\)

a: Sửa đề: BC=10cm và ΔABC vuông tại A
\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=3\cdot8=24\left(cm^2\right)\)
b: Kẻ AH vuông góc BC
\(S_{ABM}=\dfrac{1}{2}\cdot AH\cdot BM\)
\(S_{ACM}=\dfrac{1}{2}\cdot AH\cdot CM\)
mà BM=CM
nên \(S_{ABM}=S_{ACM}\)

a/ Theo tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy ta có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{m}{n}\)
Hai tam giác ABD và tam giác ACD có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{BD}{CD}=\frac{m}{n}\)
b/ Ta có
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{m}{n}\Rightarrow\frac{S_{\Delta ABD}}{m}=\frac{S_{\Delta ACD}}{n}=\frac{S_{\Delta ABD}+S_{\Delta ACD}}{m+n}=\frac{S_{\Delta ABC}}{m+n}=\frac{s}{m+n}\)
\(\Rightarrow S_{\Delta ABD}=\frac{sm}{m+n}\)
Xét hai tam giác ABM và tam giác ABC có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{S_{\Delta ABC}}{2}=\frac{s}{2}\)
Mà \(S_{\Delta ADM}=S_{\Delta ABM}-S_{\Delta ABD}=\frac{s}{2}-\frac{sm}{m+n}\)

Tự vẽ hình~
Xét tam giác ABC và tam giác DFE
\(\frac{AB}{EF}=\frac{6}{12}=\frac{1}{2}\)
\(\frac{AC}{FE}=\frac{9}{18}=\frac{1}{2}\)
\(\frac{BC}{DE}=\frac{12}{24}=\frac{1}{2}\)
\(\Rightarrow\frac{AB}{DF}=\frac{AC}{FE}=\frac{BC}{DE}=\frac{1}{2}\)
=>Tam giác ABC đồng đang với tam giác DFE (c.c.c)

Ta có: S tg ABM =1/2 BM.AH
S tg ACM =1/2 CM.AH
Mà BM =CM(AM là đường trung tuyến )
Suy ra: Diện tích ABM= diện tích ACM.
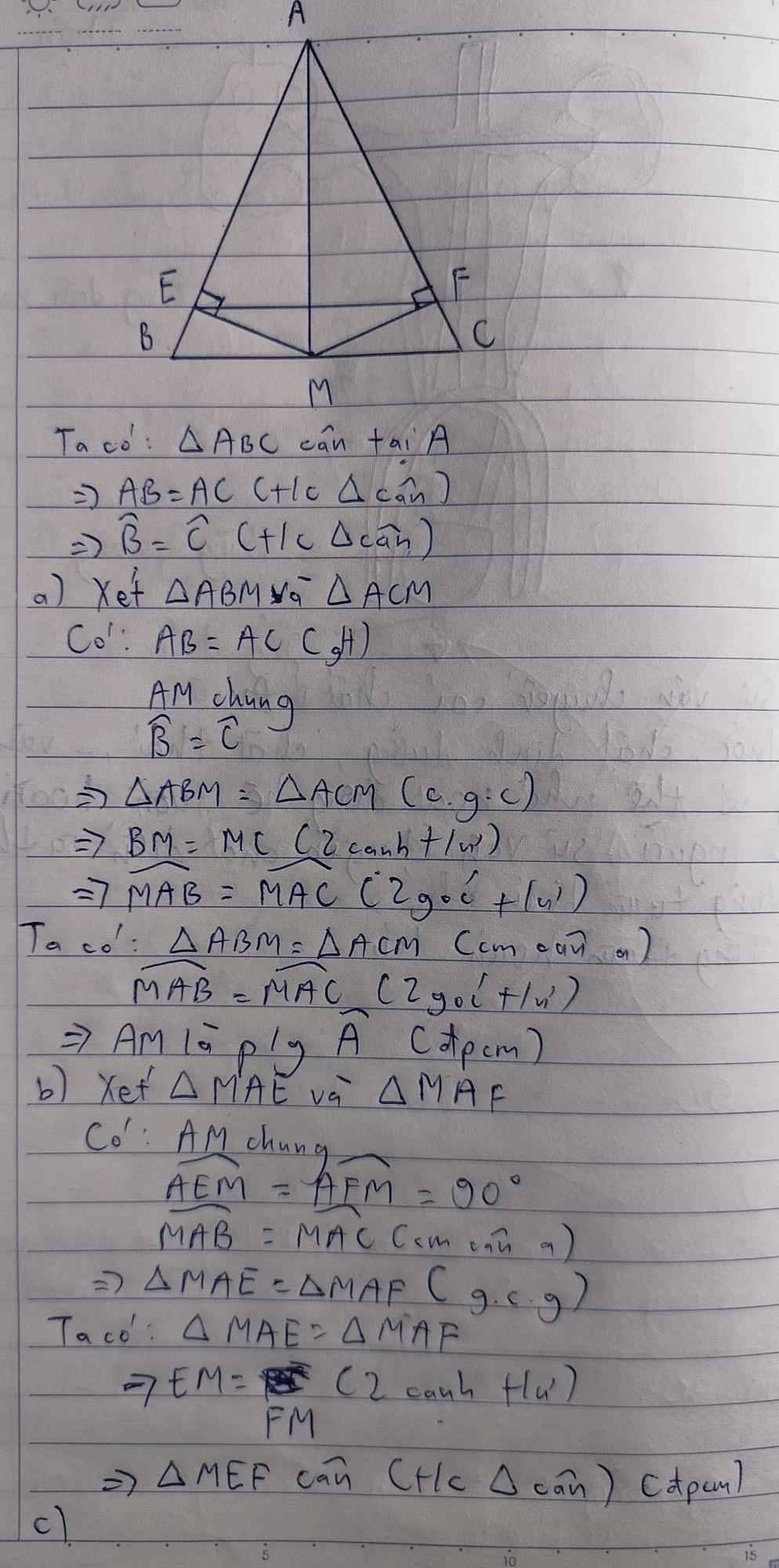
Trang cũng đăng câu này à?