Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó; E là trung điểm của AB
Xét ΔBAC có
D là trung điểm của BC
DF//AB
Do đó: F là trung điểm của AC
Xét tứ giác ADBM có
E là trung điểm chung của AB và DM
=>ADBM là hình bình hành
c: Xét tứ giác ADCN có
F là trung điểm chung của AC và DN
=>ADCN là hình bình hành
=>AN//CD và AN=CD
Ta có: ADBM là hình bình hành
=>AM//BD và AM=BD
Ta có: AN//CD
AM//BD
mà B,D,C thẳng hàng
nên AN//BC và AM//BC
mà AN,AM có điểm chung là A
nên N,A,M thẳng hàng
Ta có: AM=BD
AN=CD
mà BD=DC
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN

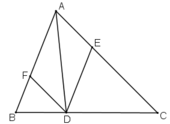
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
mà AD là tia phân giác
nên AEDF là hình thoi

-Ta có: DE//AB, DF//AC (gt).
\(\Rightarrow\) AEDF là hình bình hành mà AD là tia phân giác của \(\widehat{BAC}\) (gt).
\(\Rightarrow\) AEDF là hình thoi.
-Xét △ABC có: DF//AC (gt).
\(\Rightarrow\dfrac{BF}{AB}=\dfrac{DF}{AC}\) (định lí Ta-let).
\(\Rightarrow1-\dfrac{DF}{AB}=\dfrac{DF}{AC}\)
\(\Rightarrow\dfrac{DF}{AB}+\dfrac{DF}{AC}=1\)
\(\Rightarrow DF.\left(\dfrac{1}{AB}+\dfrac{1}{AC}\right)=1\)
\(\Rightarrow DF.\left(\dfrac{1}{3}+\dfrac{1}{6}\right)=1\)
\(\Rightarrow DF.\dfrac{1}{2}=1\)
\(\Rightarrow DF=2\) (cm).
\(\Rightarrow P_{AEDF}=4.DF=4.2=8\left(cm\right)\) (do AEDF là hình thoi).

( Bạn tự vẽ hình nha )
a) Xét tứ giác AEDF có :
DE // AB
DF // AC
=> AEDF là hình bình hành ( dấu hiệu nhận biết )
Xét hình bình hành AEDF có :
AD là phân giác của góc BAC
=> EFGD là hình thoi ( dấu hiệu nhận biết )
b) XÉt tứ giác EFGD có :
FG // ED ( AF //ED )
FG = ED ( AF = ED )
=> EFGD là hình bình hành ( dấu hiệu nhận biết )
c) Nối G với I
+) XÉt tứ giác AIGD có :
F là trung điểm của AG
F là trung điểm của ID
=> AIGD là hình bình hành ( dấu hiệu nhận biết )
=> GD // IA hay GD // AK ( tính chất )
+) Xét tứ giác AKDG có :
GD // AK
AG // Dk ( AF // ED )
=> AKDG là hình bình hành ( dấu hiệu )
+) xtes hinhnf bình hành AKDG có :
AD và GK là 2 đường chéo
=> AD và GK cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm của AD ( vì AFDE là hình thoi )
=> O là trung điểm của GK
=> ĐPCM

a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
b: Để AEDF là hình thang vuông thì góc A=90 độ

Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành